括号生成

[Bulandent]

难度：中等
来源：22. 括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

提示：

1 <= n <= 8

思路：

• 看到有效组合就可以考虑使用回溯算法的思路进行求解；
• 回溯算法 3 要素：找路径、选择列表、判断结束。
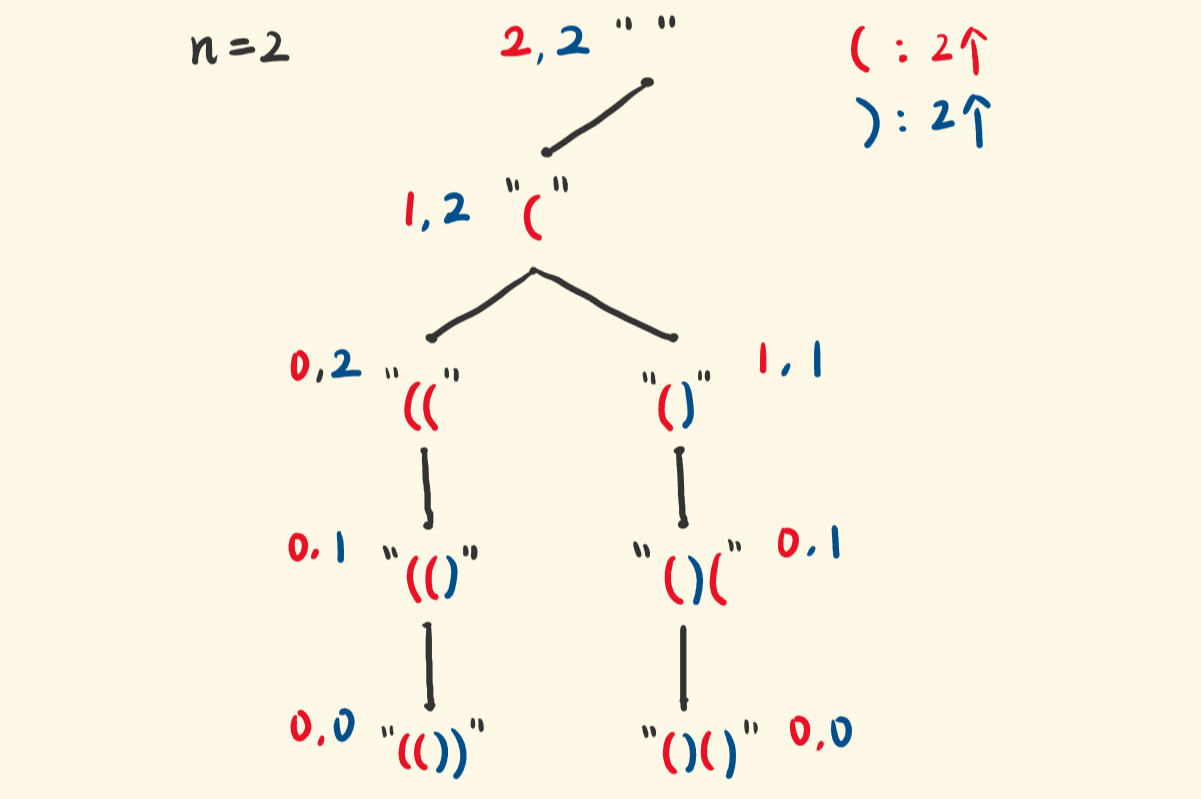
• 在这道题里：路径就是括号的组合成的字符串；列表就是二叉树的分支知道什么时候应该走左边，什么时候走右边；而判断结束的要点就是 n 的2倍和当前路径的长度相等的时候，比如 n = 1 则路径 () 的长度为 2， n = 2 则路径 ()() 的长度为 4 ，路径的最大长一定是 n 的 2 倍的，这是一个很重要的条件。
• 在递归函数里，传递 3 个参数，分别是当前路径（字符串）、左括号剩余个数和右括号剩余个数。
• 递归函数初始调用，默认参数是路径为空字符串，左括号可以填 n 个，右括号也可以填 n 个。

题解：

/**
 * @param {number} n
 * @return {string[]}
 */
var generateParenthesis = function(n) {
    let res = []
    let dfs = (curStr, left, right) => {
        if (curStr.length === n * 2) {
            res.push(curStr)
            return
        }
        if (left > 0) {
            dfs(curStr + '(', left - 1, right)
        }
        if (right > left) {
            dfs(curStr + ')', left, right - 1)
        }
    }
    dfs('', n, n)
    return res
};