diff --git a/it/task-1.md b/it/task-1.md
new file mode 100644
index 0000000..fd273bb
--- /dev/null
+++ b/it/task-1.md
@@ -0,0 +1,35 @@
+
+
+
+
+
Artist's impression of programmers struggling with The Bug.
+
Note that proper tools may be helpful!
+
+
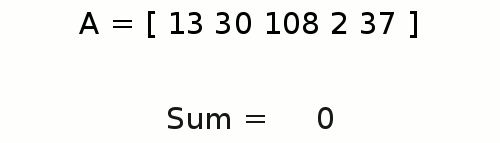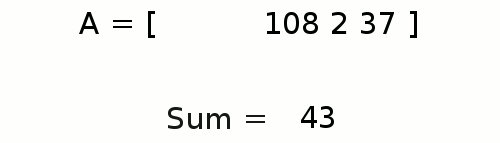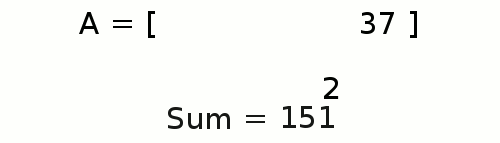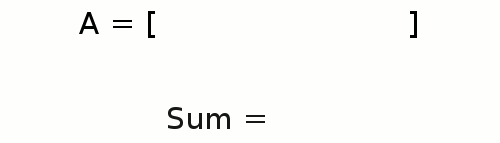
+
+

+
+
+Se hai già imparato a scrivere un programma con ciclo semplice dal problema [Sum in Loop][prevtask],
+questo nuovo esercizio sarà solo una semplice modifica.
+
+[prevtask]: ./sum-in-loop
+
+Ora ci vengono fornite diverse coppie di valori e vogliamo calcolare la somma per ciascuna coppia..
+
+**Dati di Input** conterranno in numero totale delle coppie da elaborare nella prima riga.
+Le righe successive conterranno le coppie da sommare, una coppia per riga.
+**Risposta** Dovrebbe contenere i risultati separati da spazi.
+
+Esempio:
+
+ dati:
+ 3
+ 100 8
+ 15 245
+ 1945 54
+
+ risposta:
+ 108 260 1999
+
diff --git a/it/task-36.md b/it/task-36.md
new file mode 100644
index 0000000..459a4f3
--- /dev/null
+++ b/it/task-36.md
@@ -0,0 +1,46 @@
+
+Se conoscete il vecchio gioco [Bulls and Cows](./bulls-and-cows), questo problema di programmazione vi sembrerà familiare.
+
+Andrew e Peter giocano a indovinare il codice. Andrew sceglie un `numero segreto` composto da `3` cifre. Peter cerca di
+indovinarlo, proponendo diversi valori, uno alla volta.
+
+Per ogni `ipotesi` Andrew deve dire quante cifre sono corrette, ovvero **sono le stesse** nel valore proposto e nel suo
+numero segreto, e sono posizionate nella **stessa posizione**. Ad esempio, se il numero segreto è `125` e Peter dice `523`, allora
+Andrew risponde con `1`. Ecco un esempio del gioco:
+
+ Andrea sceglie un numero segreto: 846
+
+ Ipotesi diPeter Risposta diAndrew
+ 402 0
+ 390 0
+ 816 2
+ 848 2
+ 777 0
+ 815 1
+ 846 3
+
+Quindi Peter ha indovinato il numero corretto dopo `6` tentativi.
+
+Devi scrivere un programma che legga le ipotesi fornite da Peter (tranne l'ultima) e stampi il numero segreto
+scelto da Andrew. È garantito che esista esattamente una soluzione.
+
+I **dati di input** conterranno il numero di ipotesi nella prima riga.
+Seguiranno poi le risposte con i relativi tentativi, ciascuna contenente il numero fornito da Peter e la risposta data da Andrew.
+A differenza degli esempi, i numeri saranno composti da `4` cifre.
+La **risposta** dovrebbe contenere il numero segreto (anch'esso di `4` cifre). Vedi esempio:
+
+ dat input:
+ 6
+ 402 0
+ 390 0
+ 816 2
+ 848 2
+ 777 0
+ 815 1
+
+ risposta:
+ 846
+
+
+*Qui utilizziamo valori a 3 cifre per brevità, ma l'algoritmo è lo stesso.*
+
diff --git a/it/task-39.md b/it/task-39.md
new file mode 100644
index 0000000..0407dcb
--- /dev/null
+++ b/it/task-39.md
@@ -0,0 +1,42 @@
+
+Il prolifico trader Paul Penniless vuole diventare milionario. Cerca di acquistare o vendere azioni e trarre profitto dalle
+variazioni dei prezzi. Ad esempio, se è fortunato ad acquistare `200` azioni a `20` dounds l'una e a rivenderle in una settimana a `23`,
+guadagna `600` dounds in pochi giorni.
+
+Paul ha letto un'articolo sulla [Standard Deviation](../wiki/standard-deviation) e ora ha una nuova idea. Ha subito capito
+che il problema principale è che il broker (la società che fornisce servizi per giocare al mercato) prende una commissione dell'
+1% per ogni operazione. Quindi, nell'esempio precedente, Paul perde 40` dounds quando acquista azioni e altri 46` quando le rivende.
+Quindi il profitto reale non è 600`, ma solo 600 - 40 - 46 = 514` dounds.
+
+Ora è ovvio per lui che dovrebbe preferire operazioni con azioni più **volatili**, ovvero il cui prezzo
+cambia in un intervallo più ampio, in modo che il suo profitto derivante dalle variazioni di prezzo sia più significativo
+ispetto alla commissione del broker.
+
+Ad esempio, se il prezzo iniziale delle azioni fosse stato di `50` (anziché `20`) e fosse salito a `52` quando Paul le ha vendute, il suo
+profitto per `200` azioni sarebbe stato di soli `400` dound. Tuttavia, la commissione sarebbe stata di `100` dound all'acquisto e di `104`
+dound alla vendita, quindi il suo guadagno reale sarebbe stato di soli `196` dound: più della metà del denaro è stata incassata dal broker!
+
+Paul ha deciso che avrebbe scelto se negoziare o meno azioni di un certo tipo in base alla seguente regola:
+la deviazione standard dei prezzi di queste azioni nelle ultime due settimane dovrebbe essere almeno **quattro volte maggiore** della
+commissione del broker (che è `1%`), ovvero per un'azione con prezzo medio `50` la commissione è `0,5` e la deviazione standard
+dovrebbe essere uguale o maggiore di `2`.
+
+Ad esempio, se il prezzo era `99` dound per `7` giorni e `101` per gli altri `7` giorni, il prezzo medio è `100`,
+e la commissione di intermediazione (per azione) è `1` dound. Anche la deviazione standard sarebbe `1` dound, quindi queste azioni non
+meritano di essere acquistate o vendute.
+
+**I dati di input** conterranno il numero di azioni (tipi o nomi di azioni) per cui devono essere eseguiti i calcoli.
+Le righe successive contengono le descrizioni delle azioni - il nome dell'azione (quattro lettere latine) e poi i valori `14` - i prezzi per
+ogni giorno nelle ultime due settimane.
+**La risposta** dovrebbe contenere i nomi delle azioni che sono sufficientemente volatili secondo i criteri di Paul (nello stesso ordine in cui
+sono state fornite nell'input).
+
+Esempio:
+
+ dati input:
+ 2
+ JOOG 99 99 99 99 99 99 99 101 101 101 101 101 101 101
+ GOLD 95 105 95 105 95 105 95 105 95 105 95 105 95 105
+
+ risposta:
+ GOLD
diff --git a/it/task-4.md b/it/task-4.md
new file mode 100644
index 0000000..8811e6c
--- /dev/null
+++ b/it/task-4.md
@@ -0,0 +1,34 @@
+
+
+
+

+
 +
+ +
+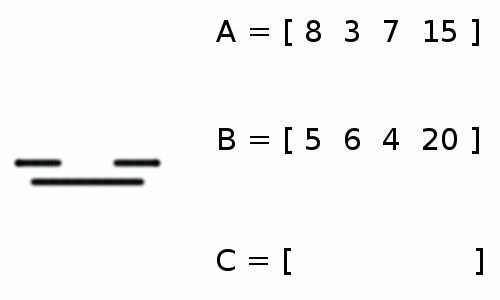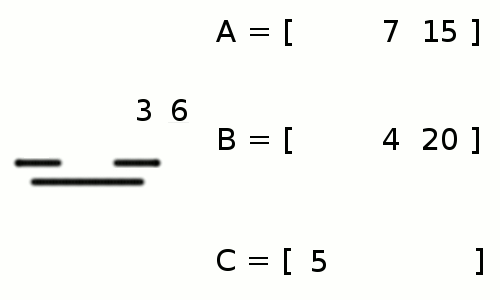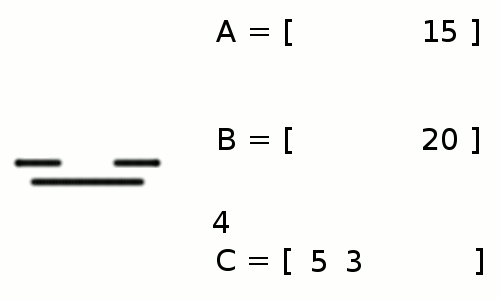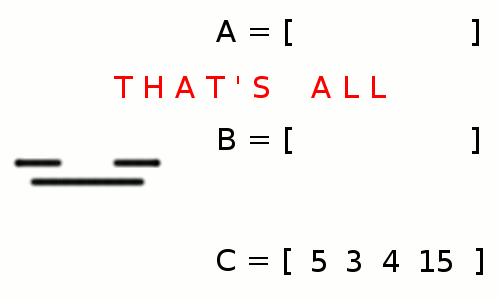 +
+ +
+