Open
Description
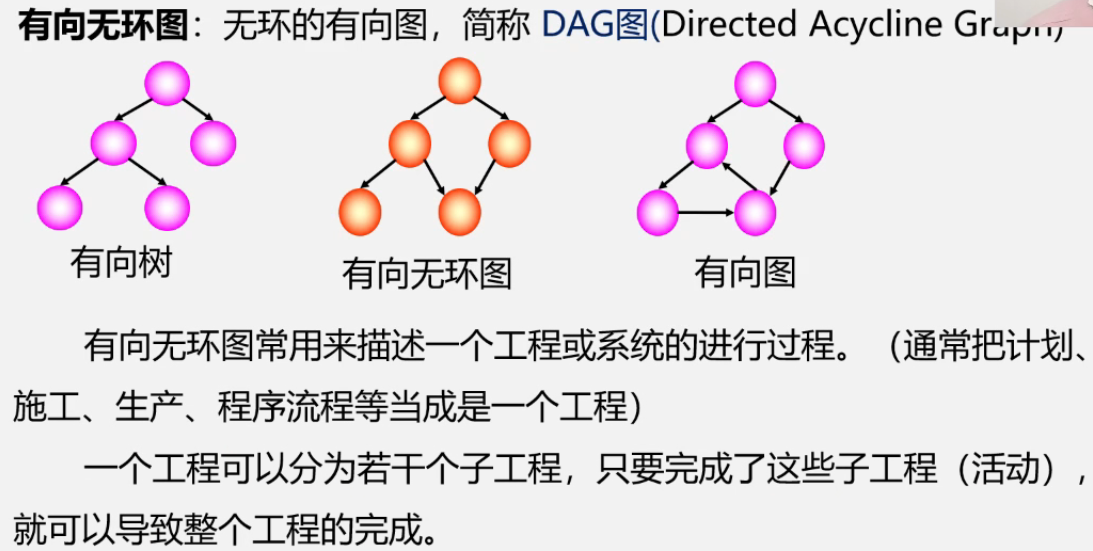
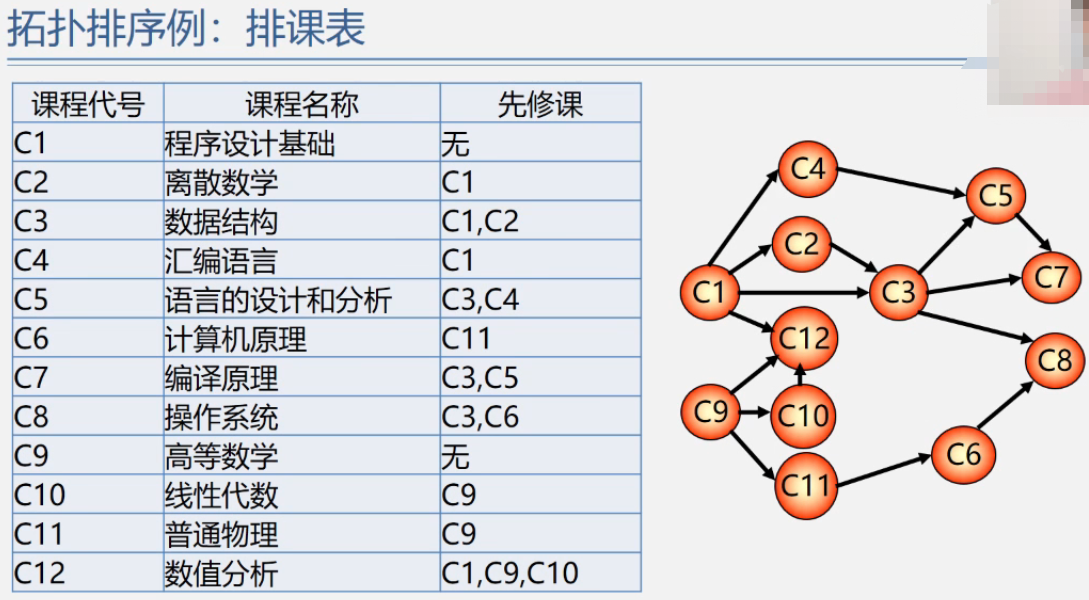
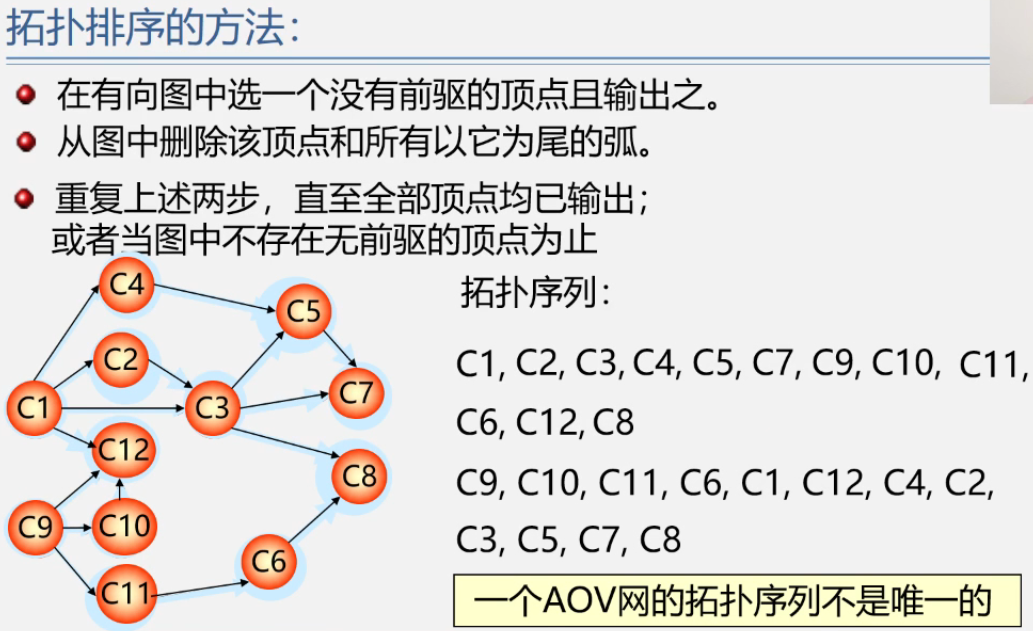
拓扑排序
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @return {boolean}
*/
const canFinish = (numCourses, prerequisites) => {
const inDegree = new Array(numCourses).fill(0); // 用于存储每个顶点的入度
const map = {} // 用来存储图的连接关系 k:顶点,v:以k为顶点的出度所连接的点
for(let i = 0; i < prerequisites.length; i++){
inDegree[prerequisites[i][0]]++;
if(map[prerequisites[i][1]]){
map[prerequisites[i][1]].push(prerequisites[i][0]); // 添加依赖它的后续课
}else{
map[prerequisites[i][1]] = [prerequisites[i][0]];
}
}
const queue = []
let num = 0; // 选课数量
for(let i = 0; i < inDegree.length; i++){ // 所有入度为0的课入列
if(inDegree[i] == 0){
queue.push(i);
}
}
while(queue.length){
let top = queue.shift(); // 当前选的课,出列
let toDegree = map[top]; // 获取这门课对应的后续课
num++;
if(toDegree){
for(let i = 0; i < toDegree.length; i++){
inDegree[toDegree[i]]--;
if(inDegree[toDegree[i]] == 0){
queue.push(toDegree[i]);
}
}
}
}
return num == numCourses;
}
最短路径
/**
* @param {number[][]} times
* @param {number} n
* @param {number} k
* @return {number}
*/
var networkDelayTime = function(times, n, k) {
const graph = new Array(n + 1).fill(0).map(m => new Array(n + 1).fill(-1));
const distance = new Array(n + 1).fill(-1); // 存储k到所有节点的距离,下标对应节点,值代表距离
const used = new Array(n + 1).fill(false);
// 初始化二维矩阵
for(let i = 0; i < times.length; i++){
graph[times[i][0]][times[i][1]] = times[i][2];
}
// k点到其他所有节点的距离
for(let i = 1; i <= n; i++){
distance[i] = graph[k][i];
}
distance[k] = 0; // 自己到自己的距离为0
used[k] = true; // k节点已被访问
// 遍历除k之外的n - 1个节点
for(let j = 1; j < n; j++){
let minDistanceNode = 1; // 默认设置为第一个节点
let minDistance = Infinity; // 到最近节点的距离
for(let i = 1; i <= n; i++){
if(!used[i] && distance[i] != -1 && distance[i] < minDistance){
minDistance = distance[i];
minDistanceNode = i;
}
}
used[minDistanceNode] = true;
for(let i = 1; i <= n; i++){
if(graph[minDistanceNode][i] != -1){
if(distance[i] != -1){
distance[i] = Math.min(distance[i], distance[minDistanceNode] + graph[minDistanceNode][i]);
}else{
// 2->4 = 2->3 + 3->4
distance[i] = distance[minDistanceNode] + graph[minDistanceNode][i];
}
}
}
}
let res = -Infinity;
for(let i = 1; i <= n; i++){
if(distance[i] == -1) return -1;
res = Math.max(res, distance[i]);
}
return res;
};