Ensemble validation issue for temperature replica exchange

[cwalker7]

I am running temperature replica exchange simulations on small coarse-grained oligomer systems (containing a single chain), and have been using an ensemble validation check on the energies for thermodynamic state pairs. This is from the physical-validation python package (https://physical-validation.readthedocs.io/en/latest/userguide.html#ensemble-validation). I am finding that for a system with 12 replicas spaced logarithmically from 200K to 300K, using LangevinDynamicsMove with replica_mixing_scheme='swap-all', n_steps=100, collision frequency=1/ps, and time_step=10fs, the ratio ln(P(U)_1/P(U)_2) is consistently about 4-5 standard deviations off from the analytical value. The physical validation code uses the pymbar DetectEquilibration function to trim the energies for each state.

I don't think it's an issue of the time step being too large, as reducing to 1fs (with n_steps set to 1000) still leads to 4-5 standard deviations for the above system.

I've tried a number of different replica exchange parameter variations: Upon increasing n_steps to 1000, increasing the friction to 10/ps, or setting the mixing scheme to 'swap-neighbor', there is much better agreement (~1 standard deviation or less from analytical value). Those are comparable to the results for replica_mixing_scheme=None (no exchanges), and for independent simulations run in openmm.

My question is - is this a matter of simply not equilibrating each replica long enough after an exchange, or could there be an underlying issue somewhere with the exchanges?

These plots summarize the results, where quantiles is standard deviation from the analytical ratio:

[cwalker7]

My code for running the simulations is something like this:

`import numpy as np
from simtk import unit 
from openmmtools.multistate import MultiStateReporter, MultiStateSampler, ReplicaExchangeSampler
from openmmtools.multistate import ReplicaExchangeAnalyzer
 
total_simulation_time=20.0*unit.nanosecond
simulation_time_step=10*unit.femtosecond
exchange_frequency=100

simulation_steps = int(np.floor(total_simulation_time / simulation_time_step))
exchange_attempts = int(np.floor(simulation_steps / exchange_frequency))
   
num_replicas = len(temperature_list)
sampler_states = list()
thermodynamic_states = list()    
   
for temperature in temperature_list:
    thermodynamic_state = openmmtools.states.ThermodynamicState(
        system=system, temperature=temperature
    )
    thermodynamic_states.append(thermodynamic_state)
    sampler_states.append(
        openmmtools.states.SamplerState(positions)
    )
    
move = openmmtools.mcmc.LangevinDynamicsMove(
    timestep=simulation_time_step,
    collision_rate=1.0/unit.picosecond,
    n_steps=exchange_frequency,
    reassign_velocities=False,
)

simulation = ReplicaExchangeSampler(mcmc_moves=move, number_of_iterations=exchange_attempts)

reporter = MultiStateReporter("output.nc", checkpoint_interval=1)
simulation.create(thermodynamic_states, sampler_states, reporter)

simulation.minimize()
simulation.run()

analyzer = ReplicaExchangeAnalyzer(reporter)

(
    replica_energies,
    unsampled_state_energies,
    neighborhoods,
    replica_state_indices,
) = analyzer.read_energies()

# Convert replica_energies to state_energies
n_particles = np.shape(reporter.read_sampler_states(iteration=0)[0].positions)[0]
T_unit = temperature_list[0].unit
temps = np.array([temp.value_in_unit(T_unit) for temp in temperature_list])
beta_k = 1 / (kB.value_in_unit(unit.kilojoule_per_mole/T_unit) * temps)
n_replicas = len(temperature_list)
for k in range(n_replicas):
    replica_energies[:, k, :] *= beta_k[k] ** (-1)

total_steps = len(replica_energies[0][0])
state_energies = np.zeros([n_replicas, total_steps])

for step in range(total_steps):
    for state in range(n_replicas):
        state_energies[state, step] = replica_energies[
            np.where(replica_state_indices[:, step] == state)[0], 0, step
        ]
        
# Physical validation is run on 'state_energies' for adjacent temperature pairs`

[mrshirts]

One comment: in theory, if I recall correctly, it should not be necessary to equilibrate after a replica switch- it should be equilibrated automatically if the swap is accepted.

[mrshirts]

@jchodera @andrrizzi @hannahbrucemacdonald any thoughts on this?

[jchodera]

Apologies for the long delay in responding to these excellent questions---we're totally bandwidth-saturated in supporting the COVID Moonshot. While we may not be able to look into this ourselves in the short term, we are about to put out a job ad to start recruiting some more software scientists to help maintain our infrastructure and field issues like this, so things will improve in the next couple of months.

It's important to note that LangevinDynamicsMove uses the openmm.LangevinIntegrator, a leapfrog form of VVVR.
By contrast LangevinSplittingDynamicsMove uses BAOAB in the velocity Verlet form (positions and velocities are synchronized).
We very much recommend LangevinSplittingDynamicsMove if you want to ensure accurate statistics, or even better, one of the Metropolized variants.

It's been a while since I've looked at the checkensemble stuff, but if it is either (1) using velocities or instantaneous temperature, or (2) sensitive to very small-scale configuration space density errors (such as harmonic bond length distributions), then it is likely the leapfrog VVVR LangevinDynamicsMove will perform poorly. As a quick test, I'd suggest trying LangevinSplittingDynamicsMove and its Metropolized form, GHMCMove, to see if that reports improvements.

For the record, I don't believe checkensemble is an appropriate way of measuring deviation from the desired configuration space density, so we do not intend to investigate this in detail based on that measure alone. The unit tests use batteries of tests based on deviations from expectations and free energies for harmonic oscillators, and we have developed more sensitive ways to measure deviation of integrators from the desired configuration or phase space distributions.

[mrshirts]

I totally understand the issues with support here. We will try LangevinSplittingDynamicsMove (or @cwalker7 , have you already tried it? I think you tried GHMCMove?

For the record, I don't believe checkensemble is an appropriate way of measuring deviation from the desired configuration space density

Can you elaborate? I mean, it literally checks whether the ratio of the sampled distributions at different temperatures are consistent with the Boltzmann distribution. If it doesn't pass this check, then the statistical mechanics are, by definition, wrong. And it works with all systems, with any size (the paper you linked seemed to have issues with a n=500 water box). and just requires lists of energies/enthalpies. Harmonic oscillator tests by definition omit anharmonic contributions, which could be problematic when working with integrators with quadratic errors. And checkensemble works with NPT as well as NVT. I definitely appreciate that the other checks are more sensitive for configuration space distributions, and can therefore pick up other more subtle errors (i.e. ergodicity), but not obeying the Boltzmann distribution is not a great feature.

using velocities or instantaneous temperature

It is not using instantaneous temperature, that is a concept that is not really applicable to statistical mechanics! The only real temperature is the specified thermostat temperature of the bath, which is what is used. @cwalker7, can you double-check and see if these tests are using the total energy or the potential energy? Some of the integrators push error into the velocities, so it would be better to use quantities that only test the configurations. I mean, both should be satisfied, but configuration is more important.

(2) sensitive to very small-scale configuration space density errors

It's a good question exactly which configuration space density errors might be responsible; we don't have a great sense. We have relatively soft harmonic bonds (I think 1000 kJ/nm^2 for the coarse-grained models systems tested here - @cwalker7 can you confirm?).
However, the effect is independent of time step over a large range (10 fs to 1 fs), so I doubt it has to do with harmonic bond length distributions, as those errors should be quite highly dependent on the time step.

Note that the errors seem to occur primarily with short exchange intervals, and that just running MD without exchanges works pretty much fine, so it does appear to have something to do with the exchanges (and any associated re-randomization?) itself, not the integrator per se.

@cwalker7, maybe you can do the "no exchange" simulations with the integrators discussed above - I suspect they will all pass the tests (maybe some slightly better than others), but the exchange simulations will all have the same problems. Would be good to see!

[jchodera]

Note that the errors seem to occur primarily with short exchange intervals, and that just running MD without exchanges works pretty much fine,

Interesting. Have you compared MultiStateSampler (same infrastructure, no exchanges) with ReplicaExchangeSampler? I'd also compare replica_mixing_scheme="swap-all" with "swap-neighbors" with None in ReplicaExchangeSampler.

Finally, are you running replica exchange serially or in parallel via MPI? We know there's a weird bug in exchanges that seems to be due to some weird mpi4py issue, but we never have been able to track it down:
#449

Please do make sure you're using potential energies (not total energies) and try the BAOAB version.

Can you elaborate? I mean, it literally checks whether the ratio of the sampled distributions at different temperatures are consistent with the Boltzmann distribution. If it doesn't pass this check, then the statistical mechanics are, by definition, wrong.

Sure, but there's no meaningful way to choose the threshold for this "check". It's not a binary thing where numbers below the threshold are "right" and numbers above the threshold are "wrong". Unless I missed a statistically meaningful approach to deciding this threshold somewhere?

[mrshirts]

Interesting. Have you compared MultiStateSampler (same infrastructure, no exchanges) with ReplicaExchangeSampler? I'd also compare replica_mixing_scheme="swap-all" with "swap-neighbors" with None in ReplicaExchangeSampler.
Finally, are you running replica exchange serially or in parallel via MPI? We know there's a weird bug in exchanges that seems to be due to some weird mpi4py issue, but we never have been able to track it down:
#449

@cwalker7 has done some of these things, but not all - @cwalker7 can you see if you can pull together the information on this?

Sure, but there's no meaningful way to choose the threshold for this "check". It's not a binary thing where numbers below the threshold are "right" and numbers above the threshold are "wrong". Unless I missed a statistically meaningful approach to deciding this threshold somewhere?

Ah, I see. So, right now our approach to assume normal error in correct simulations (which seems to be true - we should quantify this more) and look at the chance that deviations are due to random error, as there always will be some statistical deviation for any finite simulation. We then look for things that are off by too many standard deviations. Being consistently 5 standard deviations off is certainly not good.

To do this better, we could certainly do repeated samples and get better statistics. It DOES make it hard to automate for a single yes/no, since a single "off by 2.5 standard deviations" once is probably just a fluctuation, off by 2.5 standard deviations every single time indicates a subtle bug. So not so great for a unit or regression test, since if you set the cutoff too high, then you miss a lot of problems, and if you set it too low, it gets triggered far too frequently. Would be interested to hear thoughts about modifications to this.

[cwalker7]

Ok thank you very much for the comments! I will work on these additional tests today - so far I have tried the GHMCMove, and there is only marginal improvement.

Interesting. Have you compared MultiStateSampler (same infrastructure, no exchanges) with ReplicaExchangeSampler? I'd also compare replica_mixing_scheme="swap-all" with "swap-neighbors" with None in ReplicaExchangeSampler.

I haven't tried MultiStateSampler yet. One of the above plots shows 'swap-all' vs. 'swap-neighbors' vs None for ReplicaExchangeSampler, and it seems that only 'swap-all' has the issue. I can repeat this test for MultiStateSampler.

Finally, are you running replica exchange serially or in parallel via MPI? We know there's a weird bug in exchanges that seems to be due to some weird mpi4py issue, but we never have been able to track it down:

For these tests I've been running on a single GPU with openmm platform set to CUDA. If I recall, we had the same issue for multiple CPU with MPI, but I haven't tried on a single CPU.

Please do make sure you're using potential energies (not total energies) and try the BAOAB version.

I can confirm that we are using the potential energies in the physical validation (from ReplicaExchangeAnalyzer.read_energies)

We have relatively soft harmonic bonds (I think 1000 kJ/nm^2 for the coarse-grained models systems tested here - @cwalker7 can you confirm?)

Yep - that is correct.

[jchodera]

Ok, this suggests something is going on with the compiled swap-all code. Let me take a look

[mrshirts]

and it seems that only 'swap-all' has the issue.

This is great to know. If the temperature spacing is relatively broad, then "swap-neighbors" is not that much worse than "swap-all". So at minimum we can use this approach (though "swap-neighbors" would be good to use).

[jchodera]

@mrshirts can you also take a look at the swap-all code and see if you spot any logic errors? I presume it must either be a messed up array representation or weird compilation issue

[mrshirts]

Basically looking over the code in _mix_replicas in multistate/replicaechange.py (and what gets called there), correct? Will look over it. Since both use _attempt_swap, my GUESS is that it's something to do with repeated swaps and the state of the system remaining partially in the pre-swap state - it LOOKS correct on first glance, but if it didn't look correct on first glance it probably would have been caught already. I'll keep digging. If we can localize the problem just here, that would be very good.

I wonder it has to do with the fact that the reduced energies may change for a state if they are now "owned" by a different temperature - the energy remains the same, but the reduced energy changes (since it is supposed to have been generated by a different temperature). I have to think through this more (and am being called away now), but that's the hypothesis I'll work through when I get a chance later today.

[jchodera]

We should be storing the replicas x states reduced potentials, which do not change after a swap. Only the assignment of state indices to replicas changes.

[jchodera]

@mrshirts Any chance you've been able to take a look at _mix_replicas()?

@jaimergp : Would you be able to help us sort out what is going on here? Or if there's a simple way we can replace the C extension with an alternative accelerator scheme that may not suffer from this issue?

[mrshirts]

So, we have three states, T0, T1, and T2, with three energies, E0, E1, and E2, where the index on the energy says where they were originally sampled from.

Then the matrix self._energy_thermodynamic_states would be, assuming row/column labels, with [replica, thermodynamic_state]

[ E0/T0 E0/T1 E0/T2 ]
[ E1/T0 E1/T1 E1/T2 ]
[ E2/T0 E2/T1 E2/T2 ]

So that the E labels correspond to replicas labels, and the T labels correspond to thermodynamic state labels.

If we start with self._replica_thermodynamic_states = [0 1 2]

Then:
self._energy_thermodynamic_states[1, self._replica_thermodynamic_states[1]] = E1/T1
self._energy_thermodynamic_states[2, self._replica_thermodynamic_states[1]] = E2/T1
self._energy_thermodynamic_states[1, self._replica_thermodynamic_states[2]] = E1/T2

Let's say we swap states 0 and 1 on the first pass. This is implemented by a swap in self.replica_thermodynamic_states, which results in self._replica_thermodynamic_states = [1 0 2]

The next time an exchange is attempted without moving, then the energies stay the same (mod labeling). Let's say the exchange is between 1 and 2 this time. The probability calculation performed is:

log_p_accept = - (energy_12 + energy_21) + energy_11 + energy_22

Where the energies are reduced energies calculated by:

energy_12 = self._energy_thermodynamic_states[replica_i=1, self._replica_thermodynamic_states[replica_i=2]].
energy_21 = self._energy_thermodynamic_states[replica_i=2, self._replica_thermodynamic_states[replica_i=1]].
energy_11 = self._energy_thermodynamic_states[replica_i=1, self._replica_thermodynamic_states[replica_i=1]].
energy_22 = self._energy_thermodynamic_states[replica_i=2, self._replica_thermodynamic_states[replica_i=2]].

Without a swap, log_p_accept = -(E1/T2 + E2/T1) + E1/T2 + E2/T2, which is correct; the difference in total log probability if we swapped the states.

Since self._replica_thermodynamic_states[1]=0 self._replica_thermodynamic_states[0]=1 and after the swap, this seems to be:

energy_12 = E1/T2
energy_21 = E2/T0
energy_11 = E1/T0
energy_22 = E2/T2

So log_p_accept = -(E1/T1 + E2/T0) + E1/T0 + E2/T2

But that's doesn't seem like the comparison that should be done. It seems like it should be:

log_p_accept = -(E0/T2 + E2/T1) + E0/T1 + E2/T2, where the denominators are the same before the swap, but where we swap E1 in place of E2.

So we should be swapping energies, but it's swapping temperatures. So it seems it should be reassigning replica labels after each swap, not thermodynamic state labels.

Does this make sense? Am I missing something? I'm a little tired, so I'm not quite sure in the context of the objects what the solution would be.

[jchodera]

This logic doesn't sound right to me.

Fundamentally, we're dealing with the unnormalized probability density

q(S; X) = \exp{- \sum_{k=1}^K u_{s_k}(x_k)] }

where S = {s_k} is the permutation of state indices, s_k denotes the state index of replica k, u_s(x) is the reduced potential for snapshot x, and X = {x_k} is the set of snapshots, where x_k denotes the snapshot of replica k.

When we accept or reject a proposal from S -> S', we just need to compute

P_accept = \max\{ 1, q(S' | X) / q(S | X) \}

The expressions we use in the code just implicitly cancel out the terms that do not change in the swap.

I still feel like something weird must be going on in the cython code. Have we been able to try it without that, with the pure python implementation? You can just delete the Cython compiled versions from the Python installation, I think, or change these lines to always use the pure python version.

I've just tested the pure Python implementation with a 3-state test, and it seems to be totally correct empirically, as well as mathematically.

[jchodera]

I've made some progress in creating a numba jit alternative that is just as readable as the original Python version. On 100 states, the timing is

• Python: 9.6 s
• cython: 4.1 s
• numba: 0.04 s

Seems to be worth switching, since it also gets rid of the cython problems we've been having. I'll open a PR.

EDIT: Here's a notebook that illustrates what I've done.

[jaimergp]

Wow, that's insane!

[jchodera]

@cwalker7 : Thanks so much for your patience---it took a while for me to get to this!

Can you try out the fix-mixing branch to see if it resolves this?
Note that you'll have to conda install numba first.

[jchodera]

@cwalker7 : I've merged #485 in, so you should give master a try instead.

[cwalker7]

@jchodera Ok I should have the results later this afternoon - thanks for working on this!

[jchodera]

@cwalker7: Just wondering if this was able to fix things for you! The harmonic oscillator tests seem to be working fine.

[cwalker7]

This is the result using the numba swap-all. Unfortunately it is about the same deviation from the analytical values as before. Updating the plot above, we see:

I haven't yet tried the pure python version.

[jchodera]

Thanks for the update! I'll continue investigating this.

[mrshirts]

Chris, can you test the pure python version? I can then try a fix (I think I know how to do it - just have to remember how I did it in GROMACS 7-8 years ago . . . )

[jchodera]

@mrshirts : I still don't understand what you think is wrong. I'm happy to implement it if you have can explain it in the mathematical language we used in the paper (see #480 (comment))

[mrshirts]

Well, it's clearly wrong since it gives the wrong distributions. I believe it's a problem of switches not actually carrying along the correct temperature since reduced potentials are being exchanged instead of potentials - it would only occur when the temperatures are different (should be fine with Hamiltonian exchange all at the same T). I'll code up what I think is wrong since I'm not being clear in my explanations (after Chris verifies the pure python, in case that version actually is right).

[cwalker7]

@jchodera Seems like ParallelTemperingSampler works! This should definitely narrow things down then:

It is also about 13% faster than ReplicaExchangeSampler this case.

[jchodera]

That's odd. Ok, @cwalker7, can you point me to the code that sets up, runs, and analyzes these simulations?

[cwalker7]

Actually I realized that the temperatures generated from setting the min_temperature, max_temperature in ParallelTemperingSampler do not match the range I provided manually for ReplicaExchangeSampler.

For the ReplicaExchangeSampler I did something like this, where temperature list goes from 200 to 300K over 12 replicas:

for temperature in temperature_list:
    thermodynamic_state = openmmtools.states.ThermodynamicState(
        system=system, temperature=temperature
    )
    thermodynamic_states.append(thermodynamic_state)
    sampler_states.append(
        openmmtools.states.SamplerState(positions)
    )
    
move = openmmtools.mcmc.LangevinDynamicsMove(
    timestep=simulation_time_step,
    collision_rate=1.0/unit.picosecond,
    n_steps=exchange_frequency,
    reassign_velocities=False,
)

simulation = ReplicaExchangeSampler(mcmc_moves=move, number_of_iterations=exchange_attempts,replica_mixing_scheme='swap-all')

reporter = MultiStateReporter("output.nc", checkpoint_interval=1)
simulation.create(thermodynamic_states, sampler_states, reporter)

For ParallelTemperSampler I am doing this:

for temperature in temperature_list:
    thermodynamic_state = openmmtools.states.ThermodynamicState(
        system=system, temperature=temperature
    )
    thermodynamic_states.append(thermodynamic_state)
    sampler_states.append(
        openmmtools.states.SamplerState(positions)
    )

move = openmmtools.mcmc.LangevinDynamicsMove(
    timestep=simulation_time_step,
    collision_rate=friction,
    n_steps=exchange_frequency,
    reassign_velocities=False,
)

simulation = ParallelTemperingSampler(
    mcmc_moves=move,
    number_of_iterations=exchange_attempts,
    replica_mixing_scheme='swap-all'
    )

reporter = MultiStateReporter(output_data, checkpoint_interval=1)
simulation.create(
    thermodynamic_states[0],
    openmmtools.states.SamplerState(positions),
    reporter,
    min_temperature=temperature_list[0],
    max_temperature=temperature_list[-1],
    n_temperatures=num_replicas,
    )

Somehow, the temperatures in the ParallelTemperingSampler come out to be [163.2, 165.1, 167.1, 169.3, 171.7, 174.3, 177.1, 180.2, 183.5, 187.1, 191.1, 195.3], instead of the expected [200, 207.5, 215.3, 223.4, 231.8, 240.5, 249.5, 258.9, 268.6, 278.7, 289.1, 300].

Can you see what I am doing wrong?

[cwalker7]

Going into the parallel tempering code, it actually does return 163.2 to 195.3 given a min of 200 and max of 300.
https://github.com/choderalab/openmmtools/blob/master/openmmtools/multistate/paralleltempering.py#L157-L159.

I though it may be this:

temperatures = [min_temperature + (max_temperature - min_temperature) *
                            (math.exp(i / (n_temperatures-1)) - 1.0) / (math.e - 1.0) for i in range(n_temperatures)]

But it does not agree with the result from the np.logspace() function.

[jchodera]

Can you share your complete code, @cwalker7?

[cwalker7]

Ok @jchodera , so I've added the files used for the above tests to the cg_openmm repo, a python package we are working on for modeling coarse-grained foldamers: https://github.com/shirtsgroup/cg_openmm.

The replica exchange simulation setup is located here: https://github.com/shirtsgroup/cg_openmm/blob/master/cg_openmm/simulation/rep_exch.py#L434. This currently uses the 'swap-neighbor' setting.

To run the replica exchange physical validation example, first you will need to install some dependencies listed here: https://github.com/shirtsgroup/cg_openmm/blob/master/devtools/conda-envs/test_env.yaml
(sorry we don't have better documentation for this part yet, but this should work with 'conda env create -f test_env.yml')

Then install cg_openmm with 'python setup.py install'.

The physical validation example is located in https://github.com/shirtsgroup/cg_openmm/tree/master/examples/physical_validation. There is a bash script which runs the replica exchange simulation, processes the data in the .nc files, and does the physical validation ensemble check.

[cwalker7]

@mrshirts @jchodera Here's a separate branch where I've re-tested the ParallelTemperingSampler with 'swap-all'. https://github.com/shirtsgroup/cg_openmm/blob/parallel_temper/cg_openmm/simulation/rep_exch.py#L434
This time, I've specified the temperature list explicitly so we can compare directly with the results for ReplicaExchangeSampler. Seems like there is once again no difference. I can post a separate issue for the automatic temperature spacing.

[jchodera]

I've fixed the temperature initialization for ParallelTemperingSampler in #148
Still looking into the other issues.

[asilveirastx]

Could it not be the case that MD would require an "equilibration" stage if the changes in temperature are too large? Maybe you could try specifying longer MD sim times between swaps and discard a fraction of steps when performing the check ensemble test.

[jchodera]

@asilveirastx:

Could it not be the case that MD would require an "equilibration" stage if the changes in temperature are too large? Maybe you could try specifying longer MD sim times between swaps and discard a fraction of steps when performing the check ensemble test.

The only equilibration that would be necessary is at the very initial burn-in phase. Once the replicas reach equilibrium, it doesn't matter if we take 1 step or 10^6 steps in between the exchanges---the exchange attempts should preserve the equilibrium ensembles.

[asilveirastx]

The only equilibration that would be necessary is at the very initial burn-in phase. Once the replicas reach equilibrium, it doesn't matter if we take 1 step or 10^6 steps in between the exchanges---the exchange attempts should preserve the equilibrium ensembles.

I think this is 100% true when you use MCMC, but there is no formal proof that this is the case for molecular dynamics. Openmmtools has an implementation of Hybrid Monte Carlo so using HMC instead of MD could also help in discarding any issue with MD.

[maxentile]

I think this is 100% true when you use MCMC, but there is no formal proof that this is the case for molecular dynamics. Openmmtools has an implementation of Hybrid Monte Carlo so using HMC instead of MD could also help in discarding any issue with MD.

Agreed -- Langevin MD, esp. at large stepsizes, can run with a different steady-state velocity distribution than the Maxwell-Boltzmann distribution at the defined temperature. If initialized with an exact equilibrium sample x, and an exact velocity sample .setVelocitiesToTemperature(), it could require equilibration again to get back to the perturbed distribution of velocities the integrator actually uses at its steady-state.

This could plausibly have complicated effects on the behavior of parallel tempering or replica exchange.

Either

(1) running for a "sufficiently large" number of steps between exchanges (which will probably be a function of the system definition, the step size, and the collision rate -- higher collision rates should re-equilibrate the velocity distribution faster, smaller step sizes should be less wrong to start with), or
(2) using a Metropolized MD variant (such as HMC or GHMC)

would help rule this out.

[maxentile]

Although @cwalker7 reported early in this thread that the results are insensitive to decreasing the stepsize by a factor of 10 and that using GHMC doesn't change the results much, which reduces my level of suspicion that this is the main factor.

[asilveirastx]

Thanks @maxentile for pointing that out. @cwalker7 which stepsize did you use for GHMC?

[cwalker7]

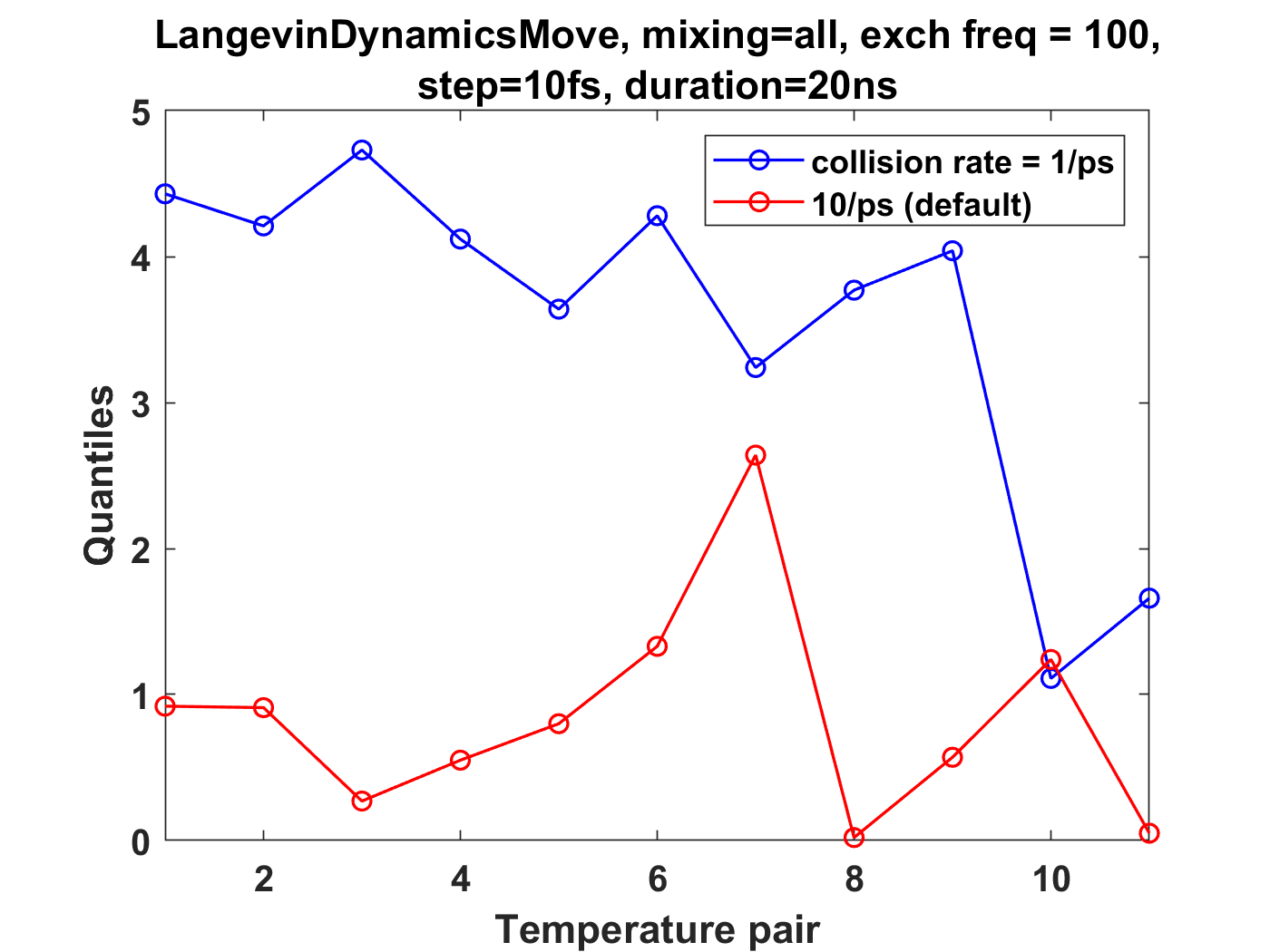
For GHMC I used a 10fs time step, exchange frequency of 100 time steps, collision rate of 1/ps, and the outcome of the ensemble check was similar to the LangevinDynamicsMove.

On the other hand, increasing the time interval between exchanges or increasing the collision rate do significantly improve the agreement with the analytical ratios (see plots 2 and 5 in the first post).

[mrshirts]

On the other hand, increasing the time interval between exchanges or increasing the collision rate do significantly improve the agreement with the analytical ratios (see plots 2 and 5 in the first post).

Which seems to indicate the something is going wrong with the exchange, and then more equilibration (or more vigorous thermal relaxation) corrects it.

[asilveirastx]

I would try HMC with a smaller time step size as this should also correct an equilibration issue

[asilveirastx]

Also @cwalker7 I'd use HMC (if your system does not have bonded terms), instead of GHMC as this last method has approximations

[cwalker7]

@asilveirastx My system does have bonded terms - I tried GHMC with step size of 1fs (keeping replica exchange frequency constant at every 1ps). The deviation is still there - the effect seems to be just reducing the noise. I'm also seeing a slowdown of about 3x in speed using GHMCMove instead of LangevinDynamicsMove (on single GPU).

[asilveirastx]

I did the analysis for a system of rigid water using HMC. The quantiles are now below 2.5, but temperatures pairs 1 and 2 are missing in the analysis because lack of overlap.

Limitations/issues of the simulations are:

1. The safe way to sample velocities would be to sample the center of mass and angular velocities for the rigid body. OpenMM uses SETTLE for constraints and atomic velocities are sampled. I am not sure if this last strategy obeys detailed balance.
2. HMC has two parameters: MD steps and stepsize. If I understood correctly, nsteps (between repex swaps) specified in move is used for MD steps in HMC. However, one should be able to specify both: HMC steps between swaps and MD steps per MC step in HMC.
3. HMC is usually very inefficient and difficult to tune as it depends on many factors (system, system size, strategy used to smooth/shift the potential, cutoff, etc.) so it would require an efficiency evaluation to determine the optimal parameters. I took the parameters from my thesis, but I used LAMMPS and rigid-body molecular dynamics. The "optimal" parameters in the current simulations are likely very different. I didn't check out the acceptance rate of HMC so I don't know the sampling quality.
   I specified one HMC step per swap, n_steps = 10 and stepsize = 3 fs. I did only 120000 replica exchange iterations, which would be 3.6 ns per replica if all HMC steps were accepted.

[mrshirts]

@asilveirastx I would expect any issue with 'swap-all' might be more obvious in the case where there was a lot of overlap, as then there will be multiple swaps up and down between states. Can you try with more overlap?

[asilveirastx]

@mrshirts yes, I'll run with more intermediate states and I'll also implement N HMC steps between swaps.

[asilveirastx]

I repeated the simulation with more intermediate states (delta T = 4 K) and I ran some preliminaries HMC simulations to check the acceptance rate for a few combination of parameters. Before running HMC, I equilibrated the water box in an NPT simulation (2 ns). The combination of stepsize = 3.5 fs and md_steps=20 yielded an acceptance rate of 0.5, which I found in my thesis to be "optimal" in the sense of obtaining more decorrelated configurations. I also specified N=40 for the number of HMC steps between repex swaps and did 10000 repex iterations. In this case I didn't have any problem of overlap and the majority of quantiles are below 1.0. I think this shows that the issue is related to the method used to sample configurations, where some MD cases introduce larger bias, and not to the swaps.

[mrshirts]

I think this shows that the issue is related to the method used to sample configurations, where some MD cases introduce larger bias, and not to the swaps.

Then why does it work for swap-neighbors, but not swap-all? That's the key issue that I'm trying to understand. I don't understand a situation in which the configurations would be OK with swap-neighbors, but not swap-all.

[asilveirastx]

Intuitively, I would say that neighbors have similar phase space distributions so that the swapped configurations will be in a similar region for both thermodynamic states. For distant thermodynamic states, MD has to pull
the configuration to the more likely region of phase space for the new thermodynamic state. I agree
that any conclusion should not be drawn based on intuition, though. So, let's try to do an analysis of transitions.
We could check a histogram of deltas in thermodynamic states indices sampled in 'swap-all' and the computed probabilities for large deltas. Let me know if you have any suggestion.

[mrshirts]

FYI, for more information, you can set pairs='all' in the physical validation script (don't need to rerun simulations, just change that setting in the analysis) That will give a LARGE number of tests, some of which will have poor overlap (like, say, i->i+20), but the comparison between the i->i+2, i->i+3, i->i+4 is usually more statistically informative if the overlap is good enough.

[oliverdutton]

Was there any resolution this issue, does 'swap_all' now function?

[jchodera]

@oliverdutton : My apologies---we haven't had time to investigate this further. I'm still uncertain if there is a problem given @asilveirastx's analysis in #480 (comment). The master branch now contains the reworked all-swap code, so there does not seem to be the potential for hidden bugs anymore.

Any other ideas as to what could be going on with the tests?

[asilveirastx]

I made histograms of the jump size for each replica in the case of rigid water where you can see that the most likely scenario is to have a jump size of 1 or 0 while a jump size = 2 only happens ~13% of the time.
I think this is the expected behavior in condensed phase systems. On the other hand, the system that @cwalker7 simulated is a chain in vacuum and the histograms show that large jump sizes in temperature are likely. I think this supports the hypothesis that large jumps in thermodynamic states, in combination with MD can introduce biases. So, I don't think there is a problem with the swap algorithm. I think the bias can be related to what @maxentile explained. I did not do the HMC simulations for the chain in vacuum because the model does not have constraints so HMC is not gonna work well.
water_jumps_histogram.pdf
vacuum_jumps_histogram_12state.pdf