Assume that file.txt has the following content:
+ Line 1 + Line 2 + Line 3 + Line 4 + Line 5 + Line 6 + Line 7 + Line 8 + Line 9 + Line 10 +
Your script should output the tenth line, which is:
+ Line 10 +
Now after pouring some non-negative integer cups of champagne, return how full the jth glass in the ith row is (both i and j are 0-indexed.)
+
Example 1:
+ Input: poured = 1, query_row = 1, query_glass = 1 + Output: 0.00000 + Explanation: We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty. +
Example 2:
+ Input: poured = 2, query_row = 1, query_glass = 1 + Output: 0.50000 + Explanation: We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange. +
Example 3:
+ Input: poured = 100000009, query_row = 33, query_glass = 17 + Output: 1.00000 +
+
Constraints:
0 <= poured <= 1090 <= query_glass <= query_row < 1000 <= poured <= 1090 <= query_glass <= query_row < 100A defanged IP address replaces every period "." with "[.]".
+
Example 1:
+Input: address = "1.1.1.1" + Output: "1[.]1[.]1[.]1" +
Example 2:
+Input: address = "255.100.50.0" + Output: "255[.]100[.]50[.]0" ++
+
Constraints:
address is a valid IPv4 address.address is a valid IPv4 address.A string is a valid parentheses string (denoted VPS) if and only if it consists of "(" and ")" characters only, and:
AB (A concatenated with B), where A and B are VPS's, or(A), where A is a VPS.AB (A concatenated with B), where A and B are VPS's, or(A), where A is a VPS.We can similarly define the nesting depth depth(S) of any VPS S as follows:
depth("") = 0depth(A + B) = max(depth(A), depth(B)), where A and B are VPS'sdepth("(" + A + ")") = 1 + depth(A), where A is a VPS.depth("") = 0depth(A + B) = max(depth(A), depth(B)), where A and B are VPS'sdepth("(" + A + ")") = 1 + depth(A), where A is a VPS.For example, "", "()()", and "()(()())" are VPS's (with nesting depths 0, 1, and 2), and ")(" and "(()" are not VPS's.
We may make the following moves:
'U' moves our position up one row, if the position exists on the board;'D' moves our position down one row, if the position exists on the board;'L' moves our position left one column, if the position exists on the board;'R' moves our position right one column, if the position exists on the board;'!' adds the character board[r][c] at our current position (r, c) to the answer.'U' moves our position up one row, if the position exists on the board;'D' moves our position down one row, if the position exists on the board;'L' moves our position left one column, if the position exists on the board;'R' moves our position right one column, if the position exists on the board;'!' adds the character board[r][c] at our current position (r, c) to the answer.(Here, the only positions that exist on the board are positions with letters on them.)
@@ -40,19 +46,31 @@ tags:Return a sequence of moves that makes our answer equal to target in the minimum number of moves. You may return any path that does so.
+
Example 1:
+Input: target = "leet" + Output: "DDR!UURRR!!DDD!" +
Example 2:
+Input: target = "code" + Output: "RR!DDRR!UUL!R!" ++
+
Constraints:
1 <= target.length <= 100target consists only of English lowercase letters.1 <= target.length <= 100target consists only of English lowercase letters.Given a 2D grid of 0s and 1s, return the number of elements in the largest square subgrid that has all 1s on its border, or 0 if such a subgrid doesn't exist in the grid.
+
Example 1:
+ Input: grid = [[1,1,1],[1,0,1],[1,1,1]] + Output: 9 +
Example 2:
+ Input: grid = [[1,1,0,0]] + Output: 1 +
+
Constraints:
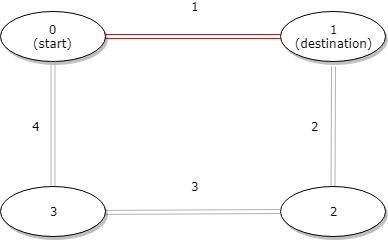
1 <= grid.length <= 1001 <= grid[0].length <= 100grid[i][j] is 0 or 11 <= grid.length <= 1001 <= grid[0].length <= 100grid[i][j] is 0 or 1Return the shortest distance between the given start and destination stops.
+
Example 1:

+ Input: distance = [1,2,3,4], start = 0, destination = 1 + Output: 1 + Explanation: Distance between 0 and 1 is 1 or 9, minimum is 1.
@@ -41,9 +45,13 @@ tags:

+ Input: distance = [1,2,3,4], start = 0, destination = 2 + Output: 3 + Explanation: Distance between 0 and 2 is 3 or 7, minimum is 3. +
@@ -53,19 +61,29 @@ tags:
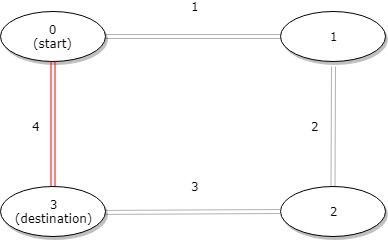
+ Input: distance = [1,2,3,4], start = 0, destination = 3 + Output: 4 + Explanation: Distance between 0 and 3 is 6 or 4, minimum is 4. +
+
Constraints:
1 <= n <= 10^4distance.length == n0 <= start, destination < n0 <= distance[i] <= 10^41 <= n <= 10^4distance.length == n0 <= start, destination < n0 <= distance[i] <= 10^4Given 2 integers n and start. Your task is return any permutation p of (0,1,2.....,2^n -1) such that :
p[0] = startp[i] and p[i+1] differ by only one bit in their binary representation.p[0] and p[2^n -1] must also differ by only one bit in their binary representation.p[0] = startp[i] and p[i+1] differ by only one bit in their binary representation.p[0] and p[2^n -1] must also differ by only one bit in their binary representation.+
Example 1:
+ Input: n = 2, start = 3 + Output: [3,2,0,1] + Explanation: The binary representation of the permutation is (11,10,00,01). + All the adjacent element differ by one bit. Another valid permutation is [3,1,0,2] +
Example 2:
+ Input: n = 3, start = 2 + Output: [2,6,7,5,4,0,1,3] + Explanation: The binary representation of the permutation is (010,110,111,101,100,000,001,011). +
+
Constraints:
1 <= n <= 160 <= start < 2 ^ n1 <= n <= 160 <= start < 2 ^ n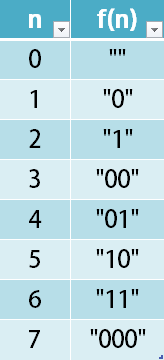
+
Example 1:
+ Input: num = 23 + Output: "1000" +
Example 2:
+ Input: num = 107 + Output: "101100" +
+
Constraints:
0 <= num <= 10^90 <= num <= 10^9In case there is no path, return [0, 0].
+
Example 1:
+Input: board = ["E23","2X2","12S"] + Output: [7,1] +
Example 2:
+Input: board = ["E12","1X1","21S"] + Output: [4,2] +
Example 3:
+Input: board = ["E11","XXX","11S"] + Output: [0,0] ++
+
Constraints:
2 <= board.length == board[i].length <= 1002 <= board.length == board[i].length <= 100Given 3 positives numbers a, b and c. Return the minimum flips required in some bits of a and b to make ( a OR b == c ). (bitwise OR operation).
+
Flip operation consists of change any single bit 1 to 0 or change the bit 0 to 1 in their binary representation.
+
Example 1:

+ Input: a = 2, b = 6, c = 5 + Output: 3 + Explanation: After flips a = 1 , b = 4 , c = 5 such that (aORb==c)
Example 2:
+ Input: a = 4, b = 2, c = 7 + Output: 1 +
Example 3:
+ Input: a = 1, b = 2, c = 3 + Output: 0 +
+
Constraints:
1 <= a <= 10^91 <= b <= 10^91 <= c <= 10^91 <= a <= 10^91 <= b <= 10^91 <= c <= 10^9Given a string s. Return all the words vertically in the same order in which they appear in s.
+
Words are returned as a list of strings, complete with spaces when is necessary. (Trailing spaces are not allowed).
+
Each word would be put on only one column and that in one column there will be only one word.
+
Example 1:
+ Input: s = "HOW ARE YOU" + Output: ["HAY","ORO","WEU"] + Explanation: Each word is printed vertically. + "HAY" + "ORO" + "WEU" +
Example 2:
+ Input: s = "TO BE OR NOT TO BE" + Output: ["TBONTB","OEROOE"," T"] + Explanation: Trailing spaces is not allowed. + "TBONTB" + "OEROOE" + " T" +
Example 3:
+ Input: s = "CONTEST IS COMING" + Output: ["CIC","OSO","N M","T I","E N","S G","T"] +
+
Constraints:
1 <= s.length <= 200s contains only upper case English letters.1 <= s.length <= 200s contains only upper case English letters.Return the restaurant's “display table”. The “display table” is a table whose row entries denote how many of each food item each table ordered. The first column is the table number and the remaining columns correspond to each food item in alphabetical order. The first row should be a header whose first column is “Table”, followed by the names of the food items. Note that the customer names are not part of the table. Additionally, the rows should be sorted in numerically increasing order.
+
Example 1:
+ Input: orders = [["David","3","Ceviche"],["Corina","10","Beef Burrito"],["David","3","Fried Chicken"],["Carla","5","Water"],["Carla","5","Ceviche"],["Rous","3","Ceviche"]] + Output: [["Table","Beef Burrito","Ceviche","Fried Chicken","Water"],["3","0","2","1","0"],["5","0","1","0","1"],["10","1","0","0","0"]] + Explanation: + The displaying table looks like: + Table,Beef Burrito,Ceviche,Fried Chicken,Water + 3 ,0 ,2 ,1 ,0 + 5 ,0 ,1 ,0 ,1 + 10 ,1 ,0 ,0 ,0 + For the table 3: David orders "Ceviche" and "Fried Chicken", and Rous orders "Ceviche". + For the table 5: Carla orders "Water" and "Ceviche". + For the table 10: Corina orders "Beef Burrito". +
Example 2:
+ Input: orders = [["James","12","Fried Chicken"],["Ratesh","12","Fried Chicken"],["Amadeus","12","Fried Chicken"],["Adam","1","Canadian Waffles"],["Brianna","1","Canadian Waffles"]] + Output: [["Table","Canadian Waffles","Fried Chicken"],["1","2","0"],["12","0","3"]] + Explanation: + For the table 1: Adam and Brianna order "Canadian Waffles". + For the table 12: James, Ratesh and Amadeus order "Fried Chicken". +
Example 3:
+ Input: orders = [["Laura","2","Bean Burrito"],["Jhon","2","Beef Burrito"],["Melissa","2","Soda"]] + Output: [["Table","Bean Burrito","Beef Burrito","Soda"],["2","1","1","1"]] +
+
Constraints:
1 <= orders.length <= 5 * 10^4orders[i].length == 31 <= customerNamei.length, foodItemi.length <= 20customerNamei and foodItemi consist of lowercase and uppercase English letters and the space character.tableNumberi is a valid integer between 1 and 500.1 <= orders.length <= 5 * 10^4orders[i].length == 31 <= customerNamei.length, foodItemi.length <= 20customerNamei and foodItemi consist of lowercase and uppercase English letters and the space character.tableNumberi is a valid integer between 1 and 500.Return the number of good nodes in the binary tree.
+
Example 1:
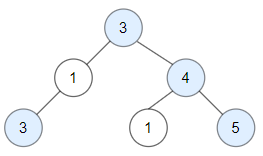
+ Input: root = [3,1,4,3,null,1,5] + Output: 4 + Explanation: Nodes in blue are good. + Root Node (3) is always a good node. + Node 4 -> (3,4) is the maximum value in the path starting from the root. + Node 5 -> (3,4,5) is the maximum value in the path + Node 3 -> (3,1,3) is the maximum value in the path.
Example 2:
@@ -44,23 +52,33 @@ Node 3 -> (3,1,3) is the maximum value in the path.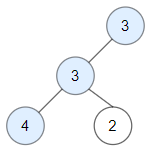
+ Input: root = [3,3,null,4,2] + Output: 3 + Explanation: Node 2 -> (3, 3, 2) is not good, because "3" is higher than it.
Example 3:
+ Input: root = [1] + Output: 1 + Explanation: Root is considered as good.
+
Constraints:
[1, 10^5].[-10^4, 10^4].[1, 10^5].[-10^4, 10^4].Return the array in the form [x1,y1,x2,y2,...,xn,yn].
+
Example 1:
+ Input: nums = [2,5,1,3,4,7], n = 3 + Output: [2,3,5,4,1,7] + Explanation: Since x1=2, x2=5, x3=1, y1=3, y2=4, y3=7 then the answer is [2,3,5,4,1,7]. +
Example 2:
+ Input: nums = [1,2,3,4,4,3,2,1], n = 4 + Output: [1,4,2,3,3,2,4,1] +
Example 3:
+ Input: nums = [1,1,2,2], n = 2 + Output: [1,2,1,2] +
+
Constraints:
1 <= n <= 500nums.length == 2n1 <= nums[i] <= 10^31 <= n <= 500nums.length == 2n1 <= nums[i] <= 10^3Given an array of integers arr and an integer k. Find the least number of unique integers after removing exactly k elements.
+
Example 1:
+ Input: arr = [5,5,4], k = 1 + Output: 1 + Explanation: Remove the single 4, only 5 is left. +Example 2:
+ Input: arr = [4,3,1,1,3,3,2], k = 3 + Output: 2 + Explanation: Remove 4, 2 and either one of the two 1s or three 3s. 1 and 3 will be left.
+
Constraints:
1 <= arr.length <= 10^51 <= arr[i] <= 10^90 <= k <= arr.length1 <= arr.length <= 10^51 <= arr[i] <= 10^90 <= k <= arr.lengthGiven two non-negative integers low and high. Return the count of odd numbers between low and high (inclusive).
+
Example 1:
+ Input: low = 3, high = 7 + Output: 3 + Explanation: The odd numbers between 3 and 7 are [3,5,7].
Example 2:
+ Input: low = 8, high = 10 + Output: 1 + Explanation: The odd numbers between 8 and 10 are [9].
+
Constraints:
0 <= low <= high <= 10^90 <= low <= high <= 10^9A triplet (arr[i], arr[j], arr[k]) is good if the following conditions are true:
0 <= i < j < k < arr.length|arr[i] - arr[j]| <= a|arr[j] - arr[k]| <= b|arr[i] - arr[k]| <= c0 <= i < j < k < arr.length|arr[i] - arr[j]| <= a|arr[j] - arr[k]| <= b|arr[i] - arr[k]| <= cWhere |x| denotes the absolute value of x.
Return the number of good triplets.
+
Example 1:
+ Input: arr = [3,0,1,1,9,7], a = 7, b = 2, c = 3 + Output: 4 + Explanation: There are 4 good triplets: [(3,0,1), (3,0,1), (3,1,1), (0,1,1)]. +
Example 2:
+ Input: arr = [1,1,2,2,3], a = 0, b = 0, c = 1 + Output: 0 + Explanation: No triplet satisfies all conditions. +
+
Constraints:
3 <= arr.length <= 1000 <= arr[i] <= 10000 <= a, b, c <= 10003 <= arr.length <= 1000 <= arr[i] <= 10000 <= a, b, c <= 1000Notice that the distance between the two cities is the number of edges in the path between them.
+
Example 1:
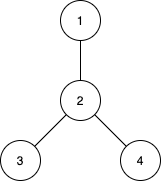
+
Input: n = 4, edges = [[1,2],[2,3],[2,4]]
+
Output: [3,4,0]
+
Explanation:
+
The subtrees with subsets {1,2}, {2,3} and {2,4} have a max distance of 1.
+
The subtrees with subsets {1,2,3}, {1,2,4}, {2,3,4} and {1,2,3,4} have a max distance of 2.
+
No subtree has two nodes where the max distance between them is 3.
+
Example 2:
+ Input: n = 2, edges = [[1,2]] + Output: [1] +
Example 3:
+ Input: n = 3, edges = [[1,2],[2,3]] + Output: [2,1] +
+
Constraints:
2 <= n <= 15edges.length == n-1edges[i].length == 21 <= ui, vi <= n(ui, vi) are distinct.2 <= n <= 15edges.length == n-1edges[i].length == 21 <= ui, vi <= n(ui, vi) are distinct.The FontInfo interface is defined as such:
+
interface FontInfo {
+
// Returns the width of character ch on the screen using font size fontSize.
+
// O(1) per call
+
public int getWidth(int fontSize, char ch);
+
+
// Returns the height of any character on the screen using font size fontSize.
+
// O(1) per call
+
public int getHeight(int fontSize);
+
}
The calculated width of text for some fontSize is the sum of every getWidth(fontSize, text[i]) call for each 0 <= i < text.length (0-indexed). The calculated height of text for some fontSize is getHeight(fontSize). Note that text is displayed on a single line.
It is also guaranteed that for any font size fontSize and any character ch:
getHeight(fontSize) <= getHeight(fontSize+1)getWidth(fontSize, ch) <= getWidth(fontSize+1, ch)getHeight(fontSize) <= getHeight(fontSize+1)getWidth(fontSize, ch) <= getWidth(fontSize+1, ch)Return the maximum font size you can use to display text on the screen. If text cannot fit on the display with any font size, return -1.
+
Example 1:
+ Input: text = "helloworld", w = 80, h = 20, fonts = [6,8,10,12,14,16,18,24,36] + Output: 6 +
Example 2:
+ Input: text = "leetcode", w = 1000, h = 50, fonts = [1,2,4] + Output: 4 +
Example 3:
+ Input: text = "easyquestion", w = 100, h = 100, fonts = [10,15,20,25] + Output: -1 +
+
Constraints:
1 <= text.length <= 50000text contains only lowercase English letters.1 <= w <= 1071 <= h <= 1041 <= fonts.length <= 1051 <= fonts[i] <= 105fonts is sorted in ascending order and does not contain duplicates.1 <= text.length <= 50000text contains only lowercase English letters.1 <= w <= 1071 <= h <= 1041 <= fonts.length <= 1051 <= fonts[i] <= 105fonts is sorted in ascending order and does not contain duplicates.Each node has three attributes:
coefficient: an integer representing the number multiplier of the term. The coefficient of the term 9x4 is 9.power: an integer representing the exponent. The power of the term 9x4 is 4.next: a pointer to the next node in the list, or null if it is the last node of the list.coefficient: an integer representing the number multiplier of the term. The coefficient of the term 9x4 is 9.power: an integer representing the exponent. The power of the term 9x4 is 4.next: a pointer to the next node in the list, or null if it is the last node of the list.For example, the polynomial 5x3 + 4x - 7 is represented by the polynomial linked list illustrated below:
The input/output format is as a list of n nodes, where each node is represented as its [coefficient, power]. For example, the polynomial 5x3 + 4x - 7 would be represented as: [[5,3],[4,1],[-7,0]].
+
Example 1:

+ Input: poly1 = [[1,1]], poly2 = [[1,0]] + Output: [[1,1],[1,0]] + Explanation: poly1 = x. poly2 = 1. The sum is x + 1. +
Example 2:
+ Input: poly1 = [[2,2],[4,1],[3,0]], poly2 = [[3,2],[-4,1],[-1,0]] + Output: [[5,2],[2,0]] + Explanation: poly1 = 2x2 + 4x + 3. poly2 = 3x2 - 4x - 1. The sum is 5x2 + 2. Notice that we omit the "0x" term. +
Example 3:
+ Input: poly1 = [[1,2]], poly2 = [[-1,2]] + Output: [] + Explanation: The sum is 0. We return an empty list. +
+
Constraints:
0 <= n <= 104-109 <= PolyNode.coefficient <= 109PolyNode.coefficient != 00 <= PolyNode.power <= 109PolyNode.power > PolyNode.next.power0 <= n <= 104-109 <= PolyNode.coefficient <= 109PolyNode.coefficient != 00 <= PolyNode.power <= 109PolyNode.power > PolyNode.next.powerGiven an integer array instructions, you are asked to create a sorted array from the elements in instructions. You start with an empty container nums. For each element from left to right in instructions, insert it into nums. The cost of each insertion is the minimum of the following:
nums that are strictly less than instructions[i].nums that are strictly greater than instructions[i].nums that are strictly less than instructions[i].nums that are strictly greater than instructions[i].For example, if inserting element 3 into nums = [1,2,3,5], the cost of insertion is min(2, 1) (elements 1 and 2 are less than 3, element 5 is greater than 3) and nums will become [1,2,3,3,5].
Return the total cost to insert all elements from instructions into nums. Since the answer may be large, return it modulo 109 + 7
+
Example 1:
+ Input: instructions = [1,5,6,2] + Output: 1 + Explanation: Begin with nums = []. + Insert 1 with cost min(0, 0) = 0, now nums = [1]. + Insert 5 with cost min(1, 0) = 0, now nums = [1,5]. + Insert 6 with cost min(2, 0) = 0, now nums = [1,5,6]. + Insert 2 with cost min(1, 2) = 1, now nums = [1,2,5,6]. + The total cost is 0 + 0 + 0 + 1 = 1.
Example 2:
+ Input: instructions = [1,2,3,6,5,4] + Output: 3 + Explanation: Begin with nums = []. + Insert 1 with cost min(0, 0) = 0, now nums = [1]. + Insert 2 with cost min(1, 0) = 0, now nums = [1,2]. + Insert 3 with cost min(2, 0) = 0, now nums = [1,2,3]. + Insert 6 with cost min(3, 0) = 0, now nums = [1,2,3,6]. + Insert 5 with cost min(3, 1) = 1, now nums = [1,2,3,5,6]. + Insert 4 with cost min(3, 2) = 2, now nums = [1,2,3,4,5,6]. + The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3. +
Example 3:
+ Input: instructions = [1,3,3,3,2,4,2,1,2] + Output: 4 + Explanation: Begin with nums = []. + Insert 1 with cost min(0, 0) = 0, now nums = [1]. + Insert 3 with cost min(1, 0) = 0, now nums = [1,3]. + Insert 3 with cost min(1, 0) = 0, now nums = [1,3,3]. + Insert 3 with cost min(1, 0) = 0, now nums = [1,3,3,3]. + Insert 2 with cost min(1, 3) = 1, now nums = [1,2,3,3,3]. + Insert 4 with cost min(5, 0) = 0, now nums = [1,2,3,3,3,4]. + Insert 2 with cost min(1, 4) = 1, now nums = [1,2,2,3,3,3,4]. + Insert 1 with cost min(0, 6) = 0, now nums = [1,1,2,2,3,3,3,4]. + Insert 2 with cost min(2, 4) = 2, now nums = [1,1,2,2,2,3,3,3,4]. + The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4. +
+
Constraints:
1 <= instructions.length <= 1051 <= instructions[i] <= 1051 <= instructions.length <= 1051 <= instructions[i] <= 105The test input is read as 3 lines:
TreeNode rootint fromNode (not available to correctBinaryTree)int toNode (not available to correctBinaryTree)TreeNode rootint fromNode (not available to correctBinaryTree)int toNode (not available to correctBinaryTree)After the binary tree rooted at root is parsed, the TreeNode with value of fromNode will have its right child pointer pointing to the TreeNode with a value of toNode. Then, root is passed to correctBinaryTree.
+
Example 1:
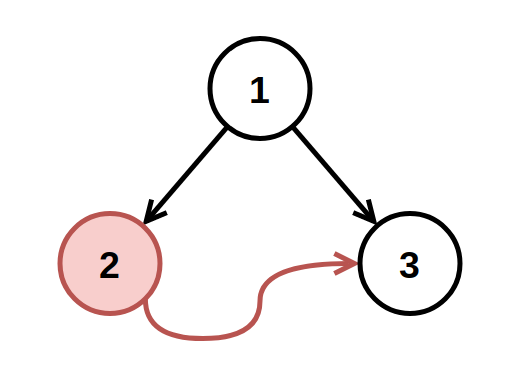
+ Input: root = [1,2,3], fromNode = 2, toNode = 3 + Output: [1,null,3] + Explanation: The node with value 2 is invalid, so remove it. +
Example 2:
@@ -52,22 +61,35 @@ tags:
+ Input: root = [8,3,1,7,null,9,4,2,null,null,null,5,6], fromNode = 7, toNode = 4 + Output: [8,3,1,null,null,9,4,null,null,5,6] + Explanation: The node with value 7 is invalid, so remove it and the node underneath it, node 2. +
+
Constraints:
[3, 104].-109 <= Node.val <= 109Node.val are unique.fromNode != toNodefromNode and toNode will exist in the tree and will be on the same depth.toNode is to the right of fromNode.fromNode.right is null in the initial tree from the test data.[3, 104].-109 <= Node.val <= 109Node.val are unique.fromNode != toNodefromNode and toNode will exist in the tree and will be on the same depth.toNode is to the right of fromNode.fromNode.right is null in the initial tree from the test data.Return the number of rectangles that can make a square with a side length of maxLen.
+
Example 1:
+ Input: rectangles = [[5,8],[3,9],[5,12],[16,5]] + Output: 3 + Explanation: The largest squares you can get from each rectangle are of lengths [5,3,5,5]. + The largest possible square is of length 5, and you can get it out of 3 rectangles. +
Example 2:
+ Input: rectangles = [[2,3],[3,7],[4,3],[3,7]] + Output: 3 +
+
Constraints:
1 <= rectangles.length <= 1000rectangles[i].length == 21 <= li, wi <= 109li != wi1 <= rectangles.length <= 1000rectangles[i].length == 21 <= li, wi <= 109li != wiReturn the maximum possible subarray sum after exactly one operation. The subarray must be non-empty.
+
Example 1:
+ Input: nums = [2,-1,-4,-3] + Output: 17 + Explanation: You can perform the operation on index 2 (0-indexed) to make nums = [2,-1,16,-3]. Now, the maximum subarray sum is 2 + -1 + 16 = 17.
Example 2:
+ Input: nums = [1,-1,1,1,-1,-1,1] + Output: 4 + Explanation: You can perform the operation on index 1 (0-indexed) to make nums = [1,1,1,1,-1,-1,1]. Now, the maximum subarray sum is 1 + 1 + 1 + 1 = 4.
+
Constraints:
1 <= nums.length <= 105-104 <= nums[i] <= 1041 <= nums.length <= 105-104 <= nums[i] <= 104Return the merged string.
+
Example 1:
+ Input: word1 = "abc", word2 = "pqr" + Output: "apbqcr" + Explanation: The merged string will be merged as so: + word1: a b c + word2: p q r + merged: a p b q c r +
Example 2:
+ Input: word1 = "ab", word2 = "pqrs" + Output: "apbqrs" + Explanation: Notice that as word2 is longer, "rs" is appended to the end. + word1: a b + word2: p q r s + merged: a p b q r s +
Example 3:
+ Input: word1 = "abcd", word2 = "pq" + Output: "apbqcd" + Explanation: Notice that as word1 is longer, "cd" is appended to the end. + word1: a b c d + word2: p q + merged: a p b q c d +
+
Constraints:
1 <= word1.length, word2.length <= 100word1 and word2 consist of lowercase English letters.1 <= word1.length, word2.length <= 100word1 and word2 consist of lowercase English letters.A garden is valid if it meets these conditions:
As the appointed gardener, you have the ability to remove any (possibly none) flowers from the garden. You want to remove flowers in a way that makes the remaining garden valid. The beauty of the garden is the sum of the beauty of all the remaining flowers.
@@ -33,36 +36,53 @@ tags:Return the maximum possible beauty of some valid garden after you have removed any (possibly none) flowers.
+
Example 1:
+ Input: flowers = [1,2,3,1,2] + Output: 8 + Explanation: You can produce the valid garden [2,3,1,2] to have a total beauty of 2 + 3 + 1 + 2 = 8.
Example 2:
+ Input: flowers = [100,1,1,-3,1] + Output: 3 + Explanation: You can produce the valid garden [1,1,1] to have a total beauty of 1 + 1 + 1 = 3. +
Example 3:
+ Input: flowers = [-1,-2,0,-1] + Output: -2 + Explanation: You can produce the valid garden [-1,-1] to have a total beauty of -1 + -1 = -2. +
+
Constraints:
2 <= flowers.length <= 105-104 <= flowers[i] <= 1042 <= flowers.length <= 105-104 <= flowers[i] <= 104You are given a 2D integer array orders, where each orders[i] = [pricei, amounti, orderTypei] denotes that amounti orders have been placed of type orderTypei at the price pricei. The orderTypei is:
0 if it is a batch of buy orders, or1 if it is a batch of sell orders.0 if it is a batch of buy orders, or1 if it is a batch of sell orders.Note that orders[i] represents a batch of amounti independent orders with the same price and order type. All orders represented by orders[i] will be placed before all orders represented by orders[i+1] for all valid i.
There is a backlog that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
buy order, you look at the sell order with the smallest price in the backlog. If that sell order's price is smaller than or equal to the current buy order's price, they will match and be executed, and that sell order will be removed from the backlog. Else, the buy order is added to the backlog.sell order, you look at the buy order with the largest price in the backlog. If that buy order's price is larger than or equal to the current sell order's price, they will match and be executed, and that buy order will be removed from the backlog. Else, the sell order is added to the backlog.buy order, you look at the sell order with the smallest price in the backlog. If that sell order's price is smaller than or equal to the current buy order's price, they will match and be executed, and that sell order will be removed from the backlog. Else, the buy order is added to the backlog.sell order, you look at the buy order with the largest price in the backlog. If that buy order's price is larger than or equal to the current sell order's price, they will match and be executed, and that buy order will be removed from the backlog. Else, the sell order is added to the backlog.Return the total amount of orders in the backlog after placing all the orders from the input. Since this number can be large, return it modulo 109 + 7.
+
Example 1:
+ +
+
+ Input: orders = [[10,5,0],[15,2,1],[25,1,1],[30,4,0]] + Output: 6 + Explanation: Here is what happens with the orders: + - 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog. + - 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog. + - 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog. + - 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog. + Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6. +
Example 2:
+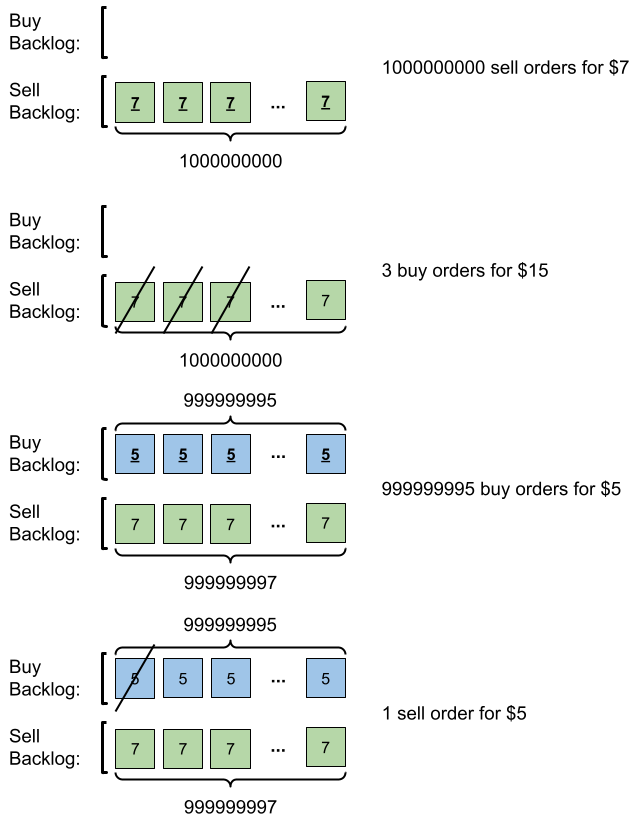 +
+
+ Input: orders = [[7,1000000000,1],[15,3,0],[5,999999995,0],[5,1,1]] + Output: 999999984 + Explanation: Here is what happens with the orders: + - 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog. + - 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog. + - 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog. + - 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog. + Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7). +
+
Constraints:
1 <= orders.length <= 105orders[i].length == 31 <= pricei, amounti <= 109orderTypei is either 0 or 1.1 <= orders.length <= 105orders[i].length == 31 <= pricei, amounti <= 109orderTypei is either 0 or 1.A nice pair is a pair (i, j) where 0 <= i < j < nums.length and low <= (nums[i] XOR nums[j]) <= high.
+
Example 1:
+
Input: nums = [1,4,2,7], low = 2, high = 6
+
Output: 6
+
Explanation: All nice pairs (i, j) are as follows:
+
- (0, 1): nums[0] XOR nums[1] = 5
+
- (0, 2): nums[0] XOR nums[2] = 3
+
- (0, 3): nums[0] XOR nums[3] = 6
+
- (1, 2): nums[1] XOR nums[2] = 6
+
- (1, 3): nums[1] XOR nums[3] = 3
+
- (2, 3): nums[2] XOR nums[3] = 5
+
Example 2:
+ Input: nums = [9,8,4,2,1], low = 5, high = 14 + Output: 8 + Explanation: All nice pairs (i, j) are as follows: + - (0, 2): nums[0] XOR nums[2] = 13 + - (0, 3): nums[0] XOR nums[3] = 11 + - (0, 4): nums[0] XOR nums[4] = 8 + - (1, 2): nums[1] XOR nums[2] = 12 + - (1, 3): nums[1] XOR nums[3] = 10 + - (1, 4): nums[1] XOR nums[4] = 9 + - (2, 3): nums[2] XOR nums[3] = 6 + - (2, 4): nums[2] XOR nums[4] = 5
+
Constraints:
1 <= nums.length <= 2 * 1041 <= nums[i] <= 2 * 1041 <= low <= high <= 2 * 1041 <= nums.length <= 2 * 1041 <= nums[i] <= 2 * 1041 <= low <= high <= 2 * 104You are given a positive integer primeFactors. You are asked to construct a positive integer n that satisfies the following conditions:
n (not necessarily distinct) is at most primeFactors.n is maximized. Note that a divisor of n is nice if it is divisible by every prime factor of n. For example, if n = 12, then its prime factors are [2,2,3], then 6 and 12 are nice divisors, while 3 and 4 are not.Return the number of nice divisors of n. Since that number can be too large, return it modulo 109 + 7.
Note that a prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. The prime factors of a number n is a list of prime numbers such that their product equals n.
+
Example 1:
+ Input: primeFactors = 5 + Output: 6 + Explanation: 200 is a valid value of n. + It has 5 prime factors: [2,2,2,5,5], and it has 6 nice divisors: [10,20,40,50,100,200]. + There is not other value of n that has at most 5 prime factors and more nice divisors. +
Example 2:
+ Input: primeFactors = 8 + Output: 18 +
+
Constraints:
1 <= primeFactors <= 1091 <= primeFactors <= 109You are given an integer array nums (0-indexed). In one operation, you can choose an element of the array and increment it by 1.
nums = [1,2,3], you can choose to increment nums[1] to make nums = [1,3,3].nums = [1,2,3], you can choose to increment nums[1] to make nums = [1,3,3].Return the minimum number of operations needed to make nums strictly increasing.
An array nums is strictly increasing if nums[i] < nums[i+1] for all 0 <= i < nums.length - 1. An array of length 1 is trivially strictly increasing.
+
Example 1:
+ Input: nums = [1,1,1] + Output: 3 + Explanation: You can do the following operations: + 1) Increment nums[2], so nums becomes [1,1,2]. + 2) Increment nums[1], so nums becomes [1,2,2]. + 3) Increment nums[2], so nums becomes [1,2,3]. +
Example 2:
+ Input: nums = [1,5,2,4,1] + Output: 14 +
Example 3:
+ Input: nums = [8] + Output: 0 +
+
Constraints:
1 <= nums.length <= 50001 <= nums[i] <= 1041 <= nums.length <= 50001 <= nums[i] <= 104Return the linked list after the deletions.
+
Example 1:
+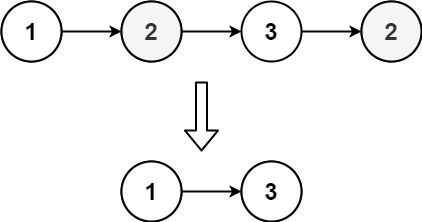 +
+
+ Input: head = [1,2,3,2] + Output: [1,3] + Explanation: 2 appears twice in the linked list, so all 2's should be deleted. After deleting all 2's, we are left with [1,3]. +
Example 2:
+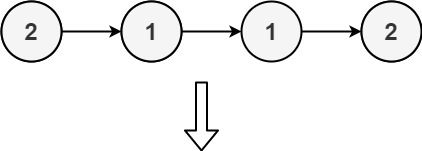 +
+
+ Input: head = [2,1,1,2] + Output: [] + Explanation: 2 and 1 both appear twice. All the elements should be deleted. +
Example 3:
+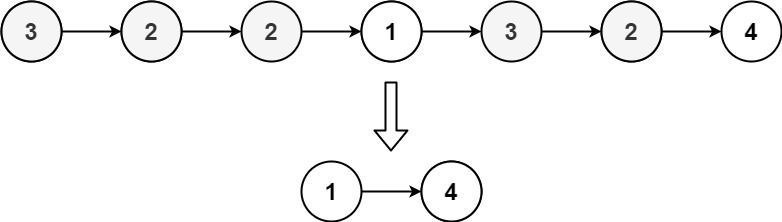 +
+
+ Input: head = [3,2,2,1,3,2,4] + Output: [1,4] + Explanation: 3 appears twice and 2 appears three times. After deleting all 3's and 2's, we are left with [1,4]. +
+
Constraints:
[1, 105]1 <= Node.val <= 105[1, 105]1 <= Node.val <= 105Return the largest color value of any valid path in the given graph, or -1 if the graph contains a cycle.
+
Example 1:
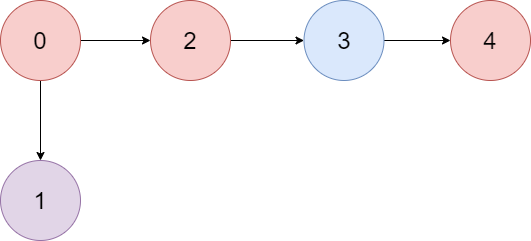
+
Input: colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]]
+
Output: 3
+
Explanation: The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored "a" (red in the above image).
+
Example 2:
@@ -47,21 +52,33 @@ tags:
+ Input: colors = "a", edges = [[0,0]] + Output: -1 + Explanation: There is a cycle from 0 to 0. +
+
Constraints:
n == colors.lengthm == edges.length1 <= n <= 1050 <= m <= 105colors consists of lowercase English letters.0 <= aj, bj < nn == colors.lengthm == edges.length1 <= n <= 1050 <= m <= 105colors consists of lowercase English letters.0 <= aj, bj < nThere are n stones arranged in a row. On each player's turn, while the number of stones is more than one, they will do the following:
x > 1, and remove the leftmost x stones from the row.x > 1, and remove the leftmost x stones from the row.The game stops when only one stone is left in the row.
@@ -39,48 +43,77 @@ tags:Given an integer array stones of length n where stones[i] represents the value of the ith stone from the left, return the score difference between Alice and Bob if they both play optimally.
+
Example 1:
+ Input: stones = [-1,2,-3,4,-5] + Output: 5 + Explanation: + - Alice removes the first 4 stones, adds (-1) + 2 + (-3) + 4 = 2 to her score, and places a stone of + value 2 on the left. stones = [2,-5]. + - Bob removes the first 2 stones, adds 2 + (-5) = -3 to his score, and places a stone of value -3 on + the left. stones = [-3]. + The difference between their scores is 2 - (-3) = 5. +
Example 2:
+ Input: stones = [7,-6,5,10,5,-2,-6] + Output: 13 + Explanation: + - Alice removes all stones, adds 7 + (-6) + 5 + 10 + 5 + (-2) + (-6) = 13 to her score, and places a + stone of value 13 on the left. stones = [13]. + The difference between their scores is 13 - 0 = 13. +
Example 3:
+ Input: stones = [-10,-12] + Output: -22 + Explanation: + - Alice can only make one move, which is to remove both stones. She adds (-10) + (-12) = -22 to her + score and places a stone of value -22 on the left. stones = [-22]. + The difference between their scores is (-22) - 0 = -22. +
+
Constraints:
n == stones.length2 <= n <= 105-104 <= stones[i] <= 104n == stones.length2 <= n <= 105-104 <= stones[i] <= 104The product sum of two equal-length arrays a and b is equal to the sum of a[i] * b[i] for all 0 <= i < a.length (0-indexed).
a = [1,2,3,4] and b = [5,2,3,1], the product sum would be 1*5 + 2*2 + 3*3 + 4*1 = 22.a = [1,2,3,4] and b = [5,2,3,1], the product sum would be 1*5 + 2*2 + 3*3 + 4*1 = 22.Given two arrays nums1 and nums2 of length n, return the minimum product sum if you are allowed to rearrange the order of the elements in nums1.
+
Example 1:
+ Input: nums1 = [5,3,4,2], nums2 = [4,2,2,5] + Output: 40 + Explanation: We can rearrange nums1 to become [3,5,4,2]. The product sum of [3,5,4,2] and [4,2,2,5] is 3*4 + 5*2 + 4*2 + 2*5 = 40. +
Example 2:
+ Input: nums1 = [2,1,4,5,7], nums2 = [3,2,4,8,6] + Output: 65 + Explanation: We can rearrange nums1 to become [5,7,4,1,2]. The product sum of [5,7,4,1,2] and [3,2,4,8,6] is 5*3 + 7*2 + 4*4 + 1*8 + 2*6 = 65. +
+
Constraints:
n == nums1.length == nums2.length1 <= n <= 1051 <= nums1[i], nums2[i] <= 100n == nums1.length == nums2.length1 <= n <= 1051 <= nums1[i], nums2[i] <= 100The pair sum of a pair (a,b) is equal to a + b. The maximum pair sum is the largest pair sum in a list of pairs.
(1,5), (2,3), and (4,4), the maximum pair sum would be max(1+5, 2+3, 4+4) = max(6, 5, 8) = 8.(1,5), (2,3), and (4,4), the maximum pair sum would be max(1+5, 2+3, 4+4) = max(6, 5, 8) = 8.Given an array nums of even length n, pair up the elements of nums into n / 2 pairs such that:
nums is in exactly one pair, andnums is in exactly one pair, andReturn the minimized maximum pair sum after optimally pairing up the elements.
+
Example 1:
+ Input: nums = [3,5,2,3] + Output: 7 + Explanation: The elements can be paired up into pairs (3,3) and (5,2). + The maximum pair sum is max(3+3, 5+2) = max(6, 7) = 7. +
Example 2:
+ Input: nums = [3,5,4,2,4,6] + Output: 8 + Explanation: The elements can be paired up into pairs (3,5), (4,4), and (6,2). + The maximum pair sum is max(3+5, 4+4, 6+2) = max(8, 8, 8) = 8. +
+
Constraints:
n == nums.length2 <= n <= 105n is even.1 <= nums[i] <= 105n == nums.length2 <= n <= 105n is even.1 <= nums[i] <= 105The alternating sum of a 0-indexed array is defined as the sum of the elements at even indices minus the sum of the elements at odd indices.
[4,2,5,3] is (4 + 5) - (2 + 3) = 4.[4,2,5,3] is (4 + 5) - (2 + 3) = 4.Given an array nums, return the maximum alternating sum of any subsequence of nums (after reindexing the elements of the subsequence).
A subsequence of an array is a new array generated from the original array by deleting some elements (possibly none) without changing the remaining elements' relative order. For example, [2,7,4] is a subsequence of [4,2,3,7,2,1,4] (the underlined elements), while [2,4,2] is not.
+
Example 1:
+ Input: nums = [4,2,5,3] + Output: 7 + Explanation: It is optimal to choose the subsequence [4,2,5] with alternating sum (4 + 5) - 2 = 7. +
Example 2:
+ Input: nums = [5,6,7,8] + Output: 8 + Explanation: It is optimal to choose the subsequence [8] with alternating sum 8. +
Example 3:
+ Input: nums = [6,2,1,2,4,5] + Output: 10 + Explanation: It is optimal to choose the subsequence [6,1,5] with alternating sum (6 + 5) - 1 = 10. +
+
Constraints:
1 <= nums.length <= 1051 <= nums[i] <= 1051 <= nums.length <= 1051 <= nums[i] <= 105The product difference between two pairs (a, b) and (c, d) is defined as (a * b) - (c * d).
(5, 6) and (2, 7) is (5 * 6) - (2 * 7) = 16.(5, 6) and (2, 7) is (5 * 6) - (2 * 7) = 16.Given an integer array nums, choose four distinct indices w, x, y, and z such that the product difference between pairs (nums[w], nums[x]) and (nums[y], nums[z]) is maximized.
Return the maximum such product difference.
+
Example 1:
+ Input: nums = [5,6,2,7,4] + Output: 34 + Explanation: We can choose indices 1 and 3 for the first pair (6, 7) and indices 2 and 4 for the second pair (2, 4). + The product difference is (6 * 7) - (2 * 4) = 34. +
Example 2:
+ Input: nums = [4,2,5,9,7,4,8] + Output: 64 + Explanation: We can choose indices 3 and 6 for the first pair (9, 8) and indices 1 and 5 for the second pair (2, 4). + The product difference is (9 * 8) - (2 * 4) = 64. +
+
Constraints:
4 <= nums.length <= 1041 <= nums[i] <= 1044 <= nums.length <= 1041 <= nums[i] <= 104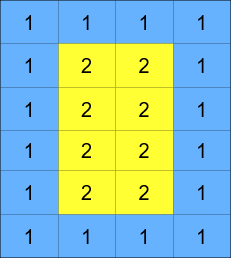
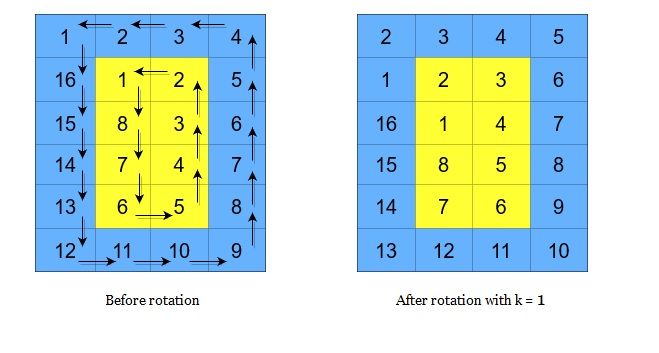
A cyclic rotation of the matrix is done by cyclically rotating each layer in the matrix. To cyclically rotate a layer once, each element in the layer will take the place of the adjacent element in the counter-clockwise direction. An example rotation is shown below:
+ +
+
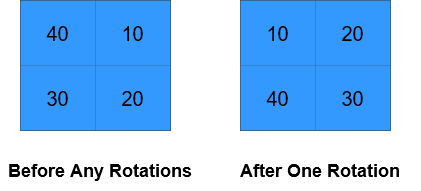
Return the matrix after applying k cyclic rotations to it.
+
Example 1:
+ +
+
+ Input: grid = [[40,10],[30,20]], k = 1 + Output: [[10,20],[40,30]] + Explanation: The figures above represent the grid at every state. +
Example 2:
+
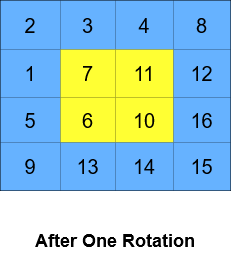
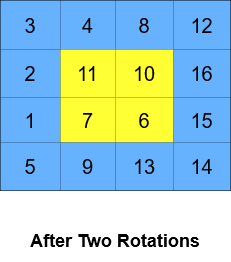
+ Input: grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], k = 2 + Output: [[3,4,8,12],[2,11,10,16],[1,7,6,15],[5,9,13,14]] + Explanation: The figures above represent the grid at every state. +
+
Constraints:
m == grid.lengthn == grid[i].length2 <= m, n <= 50m and n are even integers.1 <= grid[i][j] <= 50001 <= k <= 109m == grid.lengthn == grid[i].length2 <= m, n <= 50m and n are even integers.1 <= grid[i][j] <= 50001 <= k <= 109A wonderful string is a string where at most one letter appears an odd number of times.
"ccjjc" and "abab" are wonderful, but "ab" is not."ccjjc" and "abab" are wonderful, but "ab" is not.Given a string word that consists of the first ten lowercase English letters ('a' through 'j'), return the number of wonderful non-empty substrings in word. If the same substring appears multiple times in word, then count each occurrence separately.
A substring is a contiguous sequence of characters in a string.
+
Example 1:
+ Input: word = "aba" + Output: 4 + Explanation: The four wonderful substrings are underlined below: + - "aba" -> "a" + - "aba" -> "b" + - "aba" -> "a" + - "aba" -> "aba" +
Example 2:
+ Input: word = "aabb" + Output: 9 + Explanation: The nine wonderful substrings are underlined below: + - "aabb" -> "a" + - "aabb" -> "aa" + - "aabb" -> "aab" + - "aabb" -> "aabb" + - "aabb" -> "a" + - "aabb" -> "abb" + - "aabb" -> "b" + - "aabb" -> "bb" + - "aabb" -> "b" +
Example 3:
+ Input: word = "he" + Output: 2 + Explanation: The two wonderful substrings are underlined below: + - "he" -> "h" + - "he" -> "e" +
+
Constraints:
1 <= word.length <= 105word consists of lowercase English letters from 'a' to 'j'.1 <= word.length <= 105word consists of lowercase English letters from 'a' to 'j'.Return the number of different orders you can build all the rooms in. Since the answer may be large, return it modulo 109 + 7.
+
Example 1:
+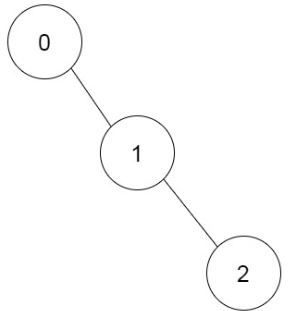 +
+
+ Input: prevRoom = [-1,0,1] + Output: 1 + Explanation: There is only one way to build the additional rooms: 0 → 1 → 2 +
Example 2:
+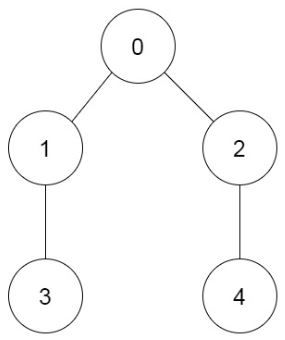
+ Input: prevRoom = [-1,0,0,1,2] + Output: 6 + Explanation: + The 6 ways are: + 0 → 1 → 3 → 2 → 4 + 0 → 2 → 4 → 1 → 3 + 0 → 1 → 2 → 3 → 4 + 0 → 1 → 2 → 4 → 3 + 0 → 2 → 1 → 3 → 4 + 0 → 2 → 1 → 4 → 3 +
+
Constraints:
n == prevRoom.length2 <= n <= 105prevRoom[0] == -10 <= prevRoom[i] < n for all 1 <= i < n0 once all the rooms are built.n == prevRoom.length2 <= n <= 105prevRoom[0] == -10 <= prevRoom[i] < n for all 1 <= i < n0 once all the rooms are built.给你一个整数 n 和一个在范围 [0, n - 1] 以内的整数 p ,它们表示一个长度为 n 且下标从 0 开始的数组 arr ,数组中除了下标为 p 处是 1 以外,其他所有数都是 0 。
给定一个整数 n 和一个整数 p,它们表示一个长度为 n 且除了下标为 p 处是 1 以外,其他所有数都是 0 的数组 arr。同时给定一个整数数组 banned ,它包含数组中的一些限制位置。在 arr 上进行下列操作:
同时给你一个整数数组 banned ,它包含数组中的一些位置。banned 中第 i 个位置表示 arr[banned[i]] = 0 ,题目保证 banned[i] != p 。
banned 中的位置上,反转大小为 k 的 子数组。返回一个包含 n 个结果的整数数组 answer,其中第 i 个结果是将 1 放到位置 i 处所需的 最少 翻转操作次数,如果无法放到位置 i 处,此数为 -1 。
-
你可以对 arr 进行 若干次 操作。一次操作中,你选择大小为 k 的一个 子数组 ,并将它 翻转 。在任何一次翻转操作后,你都需要确保 arr 中唯一的 1 不会到达任何 banned 中的位置。换句话说,arr[banned[i]] 始终 保持 0 。
示例 1:
-请你返回一个数组 ans ,对于 [0, n - 1] 之间的任意下标 i ,ans[i] 是将 1 放到位置 i 处的 最少 翻转操作次数,如果无法放到位置 i 处,此数为 -1 。
输入:n = 4, p = 0, banned = [1,2], k = 4
+ +输出:[0,-1,-1,1]
+ +解释:
i ,ans[i] 相互之间独立计算。+
示例 2:
+ +输入:n = 5, p = 0, banned = [2,4], k = 3
+ +输出:[0,-1,-1,-1,-1]
+ +解释:
+ +[0, 2] 的子数组位置上执行操作,因为位置 2 在 banned 中。示例 3:
+ +输入:n = 4, p = 2, banned = [0,1,3], k = 1
+ +输出:[-1,-1,0,-1]
+ +解释:
-示例 1:
- -
-输入:n = 4, p = 0, banned = [1,2], k = 4
-输出:[0,-1,-1,1]
-解释:k = 4,所以只有一种可行的翻转操作,就是将整个数组翻转。一开始 1 在位置 0 处,所以将它翻转到位置 0 处需要的操作数为 0 。
-我们不能将 1 翻转到 banned 中的位置,所以位置 1 和 2 处的答案都是 -1 。
-通过一次翻转操作,可以将 1 放到位置 3 处,所以位置 3 的答案是 1 。
-
-
-示例 2:
- --输入:n = 5, p = 0, banned = [2,4], k = 3 -输出:[0,-1,-1,-1,-1] -解释:这个例子中 1 一开始在位置 0 处,所以此下标的答案为 0 。 -翻转的子数组长度为 k = 3 ,1 此时在位置 0 处,所以我们可以翻转子数组 [0, 2],但翻转后的下标 2 在 banned 中,所以不能执行此操作。 -由于 1 没法离开位置 0 ,所以其他位置的答案都是 -1 。 -- -
示例 3:
- --输入:n = 4, p = 2, banned = [0,1,3], k = 1 -输出:[-1,-1,0,-1] -解释:这个例子中,我们只能对长度为 1 的子数组执行翻转操作,所以 1 无法离开初始位置。 -+
执行大小为 1 的操作,且 1 永远不会改变位置。
+