Тут размещены по 5 типов каждого задания, если решаешь все 5 — значит, с этим заданием у тебя проблем нет, ты готов. А если где-то возникают ошибки — срочно найди похожие варианты (kompege.ru) и реши их.
Легчайшее задание, просто сопоставляешь колонки из таблички с вершинами графа. При этом ориентируешься на:
— количество путей у вершины, так можно легко найти какие-то уникальные вершины в таблице (например, только 1 вершина имеет 6 путей, значит в каком-то столбце или строке в таблице 6 клеток закрашено)
— если количество путей у вершины не помогает выделить её на фоне других, смотри на количество путей у её соседей (скажем, есть 2 вершины с 3 путями, но у одной из них соседи имеют количество путей (3, 4, 2), а у другой (2, 1, 3))
— иногда бывает, что граф симметричный — это означает, что 1 раз ты можешь выбрать для равнозначных вершин любые соответствующие столбцы (есть вершины A и B с одинаковым количеством путей у них и у их соседей, и столбцы-кандидаты 2 и 3; можешь сказать "Пусть A - это 2 столбец, а B - 3" )
Алгоритм решения 2 задания состоит всего из 2 шагов:
❶ — перебираем все возможные комбинации из 0 и 1, и подставляем вместо x, y, z и w в логическую функцию
❷ — выводим те значения x, y, z, w, при которых функция давала нужный результат (1 или 0)
Общий каркас:
❶ for x in ... :
for y in ... :
for z in ... :
for w in ... :
❷ if ( ... ) == ... :
print(x, y, z, w)Реализация алгоритма:
❶ — перебор всегда осуществляется при помощи for;
все возможные подстановки 1 и 0 в x, y, z и w делаются через вложенные циклы for:
for x in 1,0:
for y in 1,0:
for z in 1,0:
for w in 1,0:
print(x, y, z, w)Если запустить данный код, получим все 16 комбинаций из 1 и 0:
Выглядеть будет так:
1 1 1 1
1 1 1 0
1 1 0 1
1 1 0 0
1 0 1 1
1 0 1 0
1 0 0 1
1 0 0 0
0 1 1 1
0 1 1 0
0 1 0 1
0 1 0 0
0 0 1 1
0 0 1 0
0 0 0 1
0 0 0 0
❷ — прямо так и пишем: "если функция такая ..., то выведи x, y, z, w"
if ((y <= z) and (not((y or w) <= (z and x)))) == 1:
print(x, y, z, w)Конечно же, логическую функцию нужно переписать с учётом синтаксиса Python:
| в заданиях | в Python |
|---|---|
|
|
or |
|
|
and |
<= |
|
== |
|
(not ... ) |
Важно: заменяя not и берём в () вместе с тем, к чему not относится.
Примеры:
| в задании | |
|---|---|
| в Python | (x or y) and (not(y == z)) and (not w) |
| в задании | |
|---|---|
| в Python | (x <= y) and (y == (not z)) and (z or w) |
| в задании | |
|---|---|
| в Python | ((not (z == w)) <= (w and (not x))) or (x and (not y)) |
Есть 2 основных типа 5 заданий, вот общая структура кода для каждого типа:
1 тип — обработка двоичной записи числа
❶ for N in range(...):
❷ N2 = bin(N)[2:]
❸ ...
❹ if ... :
A.append()
❺ print(...)-
❶ — берём число из какого-то диапазона, обычно
range(1, 1000)(еслиN- натуральное) Если программа не найдёт подходящие числа в этом диапазоне, просто берём чуть больше, напримерrange(0, 10000). Иногда диапазон указан в условии явно. -
❷ — создаём двоичную запись числа
N; для этого используемbin().bin()создаёт двоичную запись типаstr(), но с 2 ненужными первыми символами, поэтому берём срез со 2 элемента по конец[2:]. -
❸ — какие-то преобразования двоичной записи; например, добавляем какие-то символы в конец, а какие-то в начало. Часто тут есть условие — значит используем
ifиelse. -
❹ — после преобразования двоичной записи проверяем результат. Результат обычно в 10-тичной СС, для перевода в неё используем
int(..., 2). Если результат такой, какой нужно, сохраняем его — добавляем в список, например,A. -
❺ — выводим итоговый ответ. Если нам необходимо найти наименьшее подходящее число, используем
min(A), наибольшее —max(A).
2 тип — работа с 10-тичным числом
❶ for N in range(...):
❷ A = [int(x) for x in str(N)]
❸ ...
❹ if ... :
print(N)
break-
❶ — берём
Nиз диапазона; диапазон обычно явно задаётся в условии. Например, если сказано "все трёхзначные" — этоrange(100, 1000) -
❷ — раскладываем число на список его цифр:
123$\to$ [1, 2, 3]. Для чего? Чтобы было удобно делать математические операции с отдельными цифрами. -
❸ — какие-то действия с цифрами. Например, умножаем 1 и 2 цифры, 2 и 3 цифры и составляем новое число из этих произведений в порядке убывания.
-
❹ — проверяем полученный результат, если это то, что нужно, выводим. Обычно нам нужно найти наименьшее, поэтому, после вывода числа можно выйти из цикла при помощи
break.
Очень простое задание с черепахой, суть задания: посчитать количество точек в нужной области. Можно сделать в Кумир, используя пульт черепахи или нарисовать вручную.
Если в Кумир, то тебе нужно его скачать отсюда, после установки:
- заходишь в Кумир Про
- создаёшь новую программу
- ставишь галочки для черепахи и пульта в общем списке
- потом выбираешь "черепаха", у тебя появится поле для рисования
- выбираешь "пульт", с помощью него рисуешь то, что нужно
- важно: перед рисованием опусти хвост, чтобы линия была видна






Есть 2 основных типа 7 заданий:
- про изображения
- про работу с аудио
Изображения
размер изображения = размер 1 пикселя ⋅ количество пикселей
(гениально!)
Размер 1 пикселя обозначается через
размер изображения = ширина ⋅ высота
(вообще, если точно, то знак не "=", а "$⩽$")
Важно:
-
$i$ всегда измеряется в битах, поэтому и размер изображения в нашей формуле всегда переводим в биты -
количество цветов =
$2^i$ -
если изображение по условию сжимается в несколько раз, его размер уменьшается во столько же
Аудио
В этом типе мы анализируем изменение размера файла. Правило очень простое:
- какой-то параметр аудио увеличивается — во столько же раз увеличивается вес. Параметры — это частота дискретизации, количество каналов, разрешение.
Иногда ещё встречается понятие "пропускная способность". Оно тоже интуитивно понятное: чем пропускная способность выше, тем больший файл можно передать.
В этом задании составляются слова известной длины из набора каких-то символов. Нам необходимо найти из этих слов подходящие, или узнать номер нужно слова или что-то подобное.
Алгоритм здесь крайне простой:
❶ — собираем слова из букв;
по сути, генерируем все возможные комбинации из букв данного набора — разумеется, это происходит при помощи вложенных циклов for (подробнее про for тут)
Количество вложенных циклов for равно количеству букв в слове (1 цикл подставляет по очереди буквы на 1 позицию в слове)
набор, который помещаем в цикле for, составляем из уникальных букв (берём каждую по одной)
❷ — добавляем проверку условий. Для этого либо изменяем наборы в циклах for, либо пишем внутри циклов условие if
Общая структура кода:
❶ for a in "..." :
for b in "...":
for c in "...":
...
❷ if () :
счёт += 1
❸ print(счёт)-
❶ — подставляем все возможные варианты на каждую позицию в слове; сколько букв в слове — столько и вложенных циклов
for -
❷ — при помощи
ifсчитаем, сколько слов подходит под условие; когда слово подходит, увеличиваем переменнуюсчётна 1 — так мы считаем -
❸ — выводим количество подходящих слов
Пару примеров
Сколько слов длины 4, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв М, Е, Т, Р, О? Каждая буква может входить в слово несколько раз.
счёт = 0
for a in "МТР":
for b in "МЕТРО":
for c in "МЕТРО":
for d in "ЕО":
счёт += 1
print(счёт)Шифр замка — это последовательность из пяти символов, каждый из которых является цифрой от 1 до 5. Сколько различных вариантов шифра можно задать, если известно, что цифра 1 встречается ровно три раза?
счёт = 0
for a in "12345":
for b in "12345":
for c in "12345":
for d in "12345":
for e in "12345":
word = a + b + c + d + e
if word.count("1") == 3:
счёт += 1
print(счёт)Иногда слова мы собираем в алфавитном порядке.
Для этого просто в наборе в циклах for берём символы в алфавитном порядке.
Полезная вещь — для нахождения максимального, минимального, среднего и подобных вещей достаточно выделить табличку и вся информация будет в самом низу в Excel.
Алгоритм решения 11 задания:
❶ — определяем из условия, сколько символов у нас используется для кодирования
❷ — думаем, в какую степень 2 помещается это число. Эта степень имеет ровно тот же смысл, что
❸ — мы знаем вес 1 символа в битах, можем найти вес всех символов в битах
❹ — часто по условию требуется найденный нами вес всего пароля/личного кода/идентификатора поместить в минимальное целое число байт, так и делаем с числом бит из предыдущего этапа
❺ — мы знаем вес в байтах 1 пароля/личного кода/идентификатора, теперь несложно посчитать общий вес какого-то количества таких — просто умножаем
Если по заданию для 1 пользователя выдаётся несколько блоков — и личный код, и код подразделения, и доп. информация, то мы просто для каждого из этих блоков делаем этапы ❶ - ❹
Пример решения
Человеку выдаётся личный код сотрудника, код подразделения и некоторая дополнительная информация. Личный код состоит из 13 символов, каждый из которых может быть одной из 12 допустимых заглавных букв или одной из 10 цифр. Для записи личного кода используют посимвольное кодирование, все символы кодируют одинаковым минимально возможным количеством бит. Код подразделения состоит из двух натуральных чисел, не превышающих 1000, каждое из которых кодируется как двоичное число и занимает минимально возможное целое число бит. Личный код и код подразделения записываются подряд и вместе занимают минимально возможное целое число байт. Всего на пропуске хранится 32 байт данных. Сколько байт выделено для хранения дополнительных сведений об одном сотруднике?
Решение:
❶ — определяем из условия, сколько символов у нас используется для кодирования:
-
для кодирования личного кода используется по условию 12 букв и 10 цифр — всего 22 символа
-
а код подразделения — это 2 числа
$\leqslant$ 1000
❷ — думаем, в какую степень 2 помещается это число:
-
для личного кода:
$22 \leqslant 2^5$ , значит$i = 5$ — вес 1 символа в битах -
для кода подразделения: 1000
$\leqslant 2^{10}$ , значит одно такое число весит 10 бит
❸ — мы знаем вес 1 символа в битах, можем найти вес всех символов в битах:
- личный код состоит из 13 символов, если каждый весит 5 бит, то всё вместе весит:
13 ⋅ 5 = 65 бит
- код подразделения состоит из 2 чисел, каждое весит 10 бит. Всего оба числа весят 20 бит
❹ — часто по условию требуется найденный нами вес всего пароля/личного кода/идентификатора поместить в минимальное целое число байт.
Здесь в условии сказано, что личный код и код подразделения записываются в минимальное целое число байт вместе. Поэтому вначале находим их общий вес в битах и только потом его переводим в минимальное целое число байт:
65 бит + 20 бит = 85 бит
❺ — тут по условию нам дан общий вес данных для пользователя — 32 байта и необходимо найти вес доп. информации. Мы нашли, что личный код + код подразделения занимают 11 байт, значит на доп. информацию остаётся:
32 - 11 = 21 (байт) Это и есть ответ
Общая структура кода для решения такая:
❶ for x in range(...):
for y in range(...):
❷ a = .. + ".."*x + ".."*y + ...
❸ a0 = a
❹ while ".." in a:
a = a.replace("..", "..", 1)
...
❺ if ... :
print(...)❶ — эти вложенные циклы появляются, когда в строке a есть неизвестное количество каких-то символов;
1 цикл отвечает за количество конкретного символа в строке a.
❷ — собираем исходную строку a из разных символов по условию.
Например, a начинается и заканчивается "0" и в ней сколько-то символов "1":
a = "0" + "1"*x + "0"x — это переменная из цикла, она будет отвечать за количество символов "1" в строке a.
❸ — копируем исходную строку a в какую-нибудь переменную (например, в a0), если нужно
❹ — дальше полностью переписываем программу из условия на язык Python, например:
ПОКА НЕ нашлось (00)
while "00" not in a:заменить (01, 210)
a = a.replace("02", "320", 1)❺ — после того, как обработали строку a программой из условия задания, проверяем, нужный ли результат мы получили.
Например, проверим, содержится ли в нашей строке a после обработки нужное количество разных цифр и если да, выведем количество "1" в исходной строке, копию которой мы записали в a0:
if a.count("1") == 26 and a.count("2") == 54:
print(a0.count("1"))Полное решение одного 12 задания
Дана программа для редактора:
НАЧАЛО
ПОКА НЕ нашлось (00)
заменить (01, 210)
заменить (02, 320)
заменить (03, 3012)
КОНЕЦ ПОКА
КОНЕЦ
Исходная строка начиналась с нуля и заканчивалась нулём, а между ними содержала только единицы, двойки и тройки. После выполнения данной программы получилась строка из 26 единиц, 54 двойки и 48 троек.
Сколько цифр было в исходной строке?
Что означают 2 основные функции заменить() и нашлось?
Вообще, в этом задании выше есть теория, где всё и написано.
Команда заменить(a, b) работает так: заменяет строку a на строку b в исходной строке, причём заменяет только 1 раз. В Python у нас есть конструкция, которая делает то же самое — это метод .replace().
Этот метод заменяет абсолютно всё, что равно 1 аргументу на 2 аргумент:
print( "aaa".replace("a", "b") )
bbb
Как сделать так, чтобы замена происходила только 1 раз?
Для этого добавим 3, необязательный аргумент, получится .replace("a", "b", 1). Это последнее число как раз и отвечает за количество замен — в 12 задании здесь всегда пишем 1.
Команда нашлось выдаёт True, если строка, к которой мы применяем эту команду есть в нашей исходной строке.
В Python то же самое делает команда in, глянь:
print("a" in "abc")
True
print("x" in "abc")
False
Ещё в задании есть конструкция пока, её Python-овский эквивалент — цикл while.
Теперь нам просто остаётся переписать данную в условии конструкцию на язык Python.
Пусть наша исходная строка хранится в переменной a.
ПОКА НЕ нашлось (00)
while "00" not in a:
заменить (01, 210)
a = a.replace("01", "210", 1)
заменить (02, 320)
a = a.replace("02", "320", 1)
заменить (03, 3012)
a = a.replace("03", "3012", 1)
Отлично, основной каркас написан, выглядит это так:
while "00" not in a:
a = a.replace("01", "210", 1)
a = a.replace("02", "320", 1)
a = a.replace("03", "3012", 1)
Теперь осталось понять, какой была исходная строка a и что нам нужно делать в конце.
Исходная строка начиналась с нуля и заканчивалась нулём, а между ними содержала только единицы, двойки и тройки.
Создадим строку, где "0" в начале и в конце, а посередине x единиц, y двоек и z троек.
a = "0" + "1"*x + "2"*y + "3"*z + "0"x, y, z — это числа из какого-то диапазона, очень большой брать не будем, хватит range(1, 50).
Так и напишем:
for x in range(1, 50):
for y in range(1, 50):
for z in range(1, 50):
a = "0" + "1"*x + "2"*y + "3"*z + "0"
Итак, вначале мы создаём строку, где вначале и в конце "0", а между ними от 1 до 49 единиц, двоек и троек.
Потом делаем 3 замены при помощи while и .replace().
После выполнения этого кода мы получаем строку из 26 единиц, 54 двойки и 48 троек.
Как проверить, что мы получили именно такую строку?
Используем метод .count() и напишем это:
if a.count("1") == 26 and a.count("2") == 54 and a.count("3") == 48:
Если мы нашли такую строку, то, по условию, нам нужно вывести количество цифр в исходной строке.
Количество цифр — используем len(). И внутри len() у нас должна быть исходная строка.
Поскольку строка a постоянно меняется за время выполнения программы, мы должны в самом начале создать копию a, которая меняться не будет. Пусть копия называется a0. Вот и всё, код написан.
Так код выглядит в самом конце:
❶ for x in range(1, 50):
for y in range(1, 50):
for z in range(1, 50):
❷ a = "0" + "1"*x + "2"*y + "3"*z + "0"
❸ a0 = a
❹ while "00" not in a:
a = a.replace("01", "210", 1)
a = a.replace("02", "320", 1)
a = a.replace("03", "3012", 1)
❺ if a.count("1") == 26 and a.count("2") == 54 and a.count("3") == 48:
print(len(a0))❶ — берём по очереди числа от 1 до 49 — столько у нас будет единиц, двоек и троек в исходной строке a
❷ — собираем нашу строку a по условию: в начале и в конце "0", а между ними — любое количество единиц, двоек и троек от 1 до 49
❸ — копируем нашу строку a в a0, потому что потом a изменится
❹ — этот блок — дословное переписывание конструкции в условии. Меняем заменить() на .replace(), нашлось — на in. В .replace() появляется третий аргумент — 1, чтобы замена происходила только 1 раз.
❺ — проверяем, получили ли мы в строке нужное количество единиц, двоек и троек. Если да — выводим длину символов в исходной строке a0 по условию
Задание несложное, тут очень мало теории
IP - это 4 числа ≤ 255, объединённые через .; например 192.0.0.168. Разумеется в компьютере IP хранится в двоичном виде 192.0.0.168 → 11000000.00000000.00000000.10101000
Каждое из 4 двоичных чисел должно быть длины 8, если переведённое число оказалось короче, то слева числа мы дописываем 0 (101.11010.10100000.101011 → 00000101.00011010.10100000.00101011)
Раз каждое из этих 4 чисел состоит из 8 двоичных символов (бит), то эти числа можно называть байтами.
Итак, есть 1 IP сети, он даётся сети (группе устройств). Каждое из этих устройств (узлов) имеет свой IP узла.
Каким образом из 1 IP сети получается много IP узлов? — Меняются последние циферки IP сети (здесь меняются 7 последних циферок):
IP сети: 11000000.00000000.00000000.10101000
IP узлов: 11000000.00000000.00000000.11010101
11000000.00000000.00000000.11011111
....
Как понять, сколько именно последних циферок IP сети менятся? — За это отвечает маска сети.
Маска имеет ту же структуру, что и IP, но в ней вначале сплошные 1, потом с какого-то места сплошные 0, например 11111111.11111111.11110000.00000000. Так вот, сколько нулей в маске, столько последних циферок IP сети можно менять.
Например, так могут выглядеть IP сети, IP узла и маска сети:
сеть: 11000101.00011010.10111100.00101011
узел: 11000101.00011010.10111110.01101000
маска: 11111111.11111111.11111100.00000000
Маска и узел связаны ещё так: если мы сделаем конъюнкцию (умножение) каждого бита маски и каждого соответствующего бита узла, мы получим IP сети. Часть узла, которая находится над 1 в маске при конъюнкции не поменяется (ведь умножаем на 1), то есть останется такой же и в IP сети. А та часть маски, где 0 создаст нули в этом месте в IP сети (ведь умножаем на 0). То есть в IP сети в конце на месте ..... стоят нули.
узел: 11000111.00011011.10111111.11000110
↓ ↓
маска: 11111111.11111111.11111111.11100000
сеть: 11000111.00011011.10111111.110.....
1 тип — выражение из чисел в разных системах счисления
Вот полный разбор на примере:
Дано выражение наподобие x и y оно делится на 99 без остатка, и вывести, что получится при таком делении.
Алгоритм решения:
❶ — подставляем на место x и y все возможные варианты
❷ — собираем наши числа и переводим их в 10 СС
❸ — проверяем, выполняется ли условие и выводим ответ
❶ — Все возможные варианты из нескольких чисел всегда делаются при помощи вложенных циклов for, как тут.
Перебор всегда связан с циклом for.
Получаем:
for x in ... :
for y in ... :Теперь, какой набор мы используем в for.
Логика проста: в обоих наших числах есть x и y, а наши числа из какой-то системы счисления.
Любая система счисления имеет самую большую возможную цифру (гениально), выше неё цифры использовать в этой СС нельзя.
К примеру, числа
Вернёмся к нашему примеру x, y могут быть только от 0 до 10 включительно.
Смотрим на 2 число, здесь x и y могут быть только от 0 до 7 включительно.
Какой вывод? — Мы можем брать x и y только от 0 до 7.
Так и пишем:
for x in "01234567" :
for y in "01234567" :❷ — процесс сборки и перевода числа выглядит так; тут мы используем 2 аргумент int(..., ); он нужен, когда мы переводим не 10-ичный объект:
y + "04" + x + "5" int(y + "04" + x + "5") int(y + "04" + x + "5", 11)
-
1 — склеиваем отдельные строки
-
2 — преобразуем это в число —
int() -
3 — так как преобразуем в число не десятичные символы, то указываем второй аргумент в
int()— основание системы
Готово! Абсолютно аналогично собираем 2 число:
int("253" + x + y, 8)
❸ — можем прямо так и написать:
если выражение делится на 99...
if (int(y + "04" + x + "5", 11) + int("253" + x + y, 8)) % 99 == 0:Если делится, по условию нужно вывести результат деления. Так что в более полном виде получим:
if (int(y + "04" + x + "5", 11) + int("253" + x + y, 8)) % 99 == 0:
print( (...) // 99)Тут во внутренних скобках () в print() нужно будет ещё раз написать это выражение, которое в if.
В итоге, полный код выглядит так:
for x in "01234567":
for y in "01234567":
if (int(y + "04" + x + "5", 11) + int("253" + x + y, 8)) % 99 == 0:
print((int(y + "04" + x + "5", 11) + int("253" + x + y, 8)) // 99)2 тип
Вот общая схема для такого типа:
❶ число = 125 + 25**3 + 5**9
❷ while число > 0:
❸ if число % ... == ... :
счёт += 1
❹ число //= ...
❺ print(счёт) -
❶ — создаём число (просто переписываем из условия)
-
❷ — действия продолжаются, пока мы совсем не укоротили наше число
-
❸ — извлекаем последнюю цифру числа при помощи
%; если последняя цифра — нужная нам, увеличиваем какую-нибудь переменную (счёт) на 1 -
❹ — обрезаем наше число, чтобы предпоследнюю цифру тоже можно было взять через
%; это делаем в любом случае, даже если цифра нам не подошла, поэтому без отступа, не внутриif -
❺ — в самом конце, когда мы прошлись по всем цифрам
числавыводим, сколько нужных цифр мы насчитали
А вот полезное описание, почему это работает, и откуда что берётся
14 задания этого типа выглядят так:
-
дано выражение наподобие
$125 + 25^3 + 5^9$ -
нужно найти, сколько в нём каких-то цифр, если это выражение перевести в другую СС
Идея решения задания очень проста — для начала рассмотрим число
Основание этого числа и степени
Теперь, как взять из числа самую последнюю его цифру?
Помнишь, для этого мы делали число % 10.
Тут число 10 только тогда, когда число 10-тичное.
Если число будет из другой СС, то и вместо 10 будет другое число.
Например, чтобы взять последнюю цифру из числа 123 % 7.
Ок, последнюю цифру мы взяли, а как взять предпоследнюю?
Идея проста — возьмём и обрежем наше число на 1 последнюю цифру. Как мы обрезали число? Делили нацело на 10:
число // 10Здесь тоже 10 только если число в 10-тичной СС. А если число будет из другой СС, то и делить нацело будем его на другое число:
число // 7 # если число в 7-ричной ССчисло // 5 # если число в 5-ричной ССВ итоге, 2 основных действия (вместо 10 всегда пишем основание системы, в которую переводим число):
- берём последнюю цифру числа:
число % 10- обрезаем число:
число = число // 10будем писать это короче, как пишем +=:
число //= 10Эти действия повторяются до тех пор, пока число не стало из 1 символа. Так и пишем:
while число > 0:
...15 задания могут быть нескольких видов.
Вначале разберём, задания, которые звучат так: "Для какого наименьшего целого А формула .... тождественно истинна при любом целом ...."
Общая структура для решения такая:
❶ for A in range(...):
❷ stop = 0
❸ ...
❹ if stop == 0:
❺ print(A)
break❶ — берём по очереди разные A и проверяем, выполняется ли для них формула.
Важно: range() полностью зависит от условия, если по условию ищем неотрицательное целое A — то range(0, ...), а если ищем целое A — то тут range(-..., +...), например range(-100, 100)
❷ — создаём переменную stop; пусть она будет вначале 0, типо не активирована
❸ — потом делаем что-то, где stop может измениться.
А именно, берём все переменные, которые есть в формуле по условию, для каждой переменной создаём цикл for, который зависит от условия (если говорится "при любом целом x", значит range() обязательно отрицательную часть, например, range(-100, 100)).
Берём эти переменные, перебираем в цикле for и подставляем в наше выражение.
И если выражение оказывается ложным, то мы как-то меняем переменную stop:
for x in range(...):
if () == 0:
stop = 1Это мы сделали для того, чтобы на ❹ шаге проверка не была пройдена, что будет означать — такое A нам не подходит.
❹ — проверяем, если переменная stop не поменялась, значит выражение всегда выполнялось.
А значит, такое A нам подходит.
Обычно от нас требуется просто найти наименьшее подходящее A, поэтому выводим его и выходим из цикла при помощи break.
Аккуратно: не всегда нам нужно просто найти наименьшее подходящее A, иногда нужно найти что-то другое, например, их количество.
Вот пару примеров
Задание
Для какого наименьшего целого неотрицательного числа A выражение:
Решение
for A in range(0, 100):
stop = 0
for m in range(0, 100):
for n in range(0, 100):
if ((2*m + 3*n > 43) or (m < A) or (n <= A)) == 0:
stop = 1
if stop == 0:
print(A)
breakТак мы делаем 16 задание
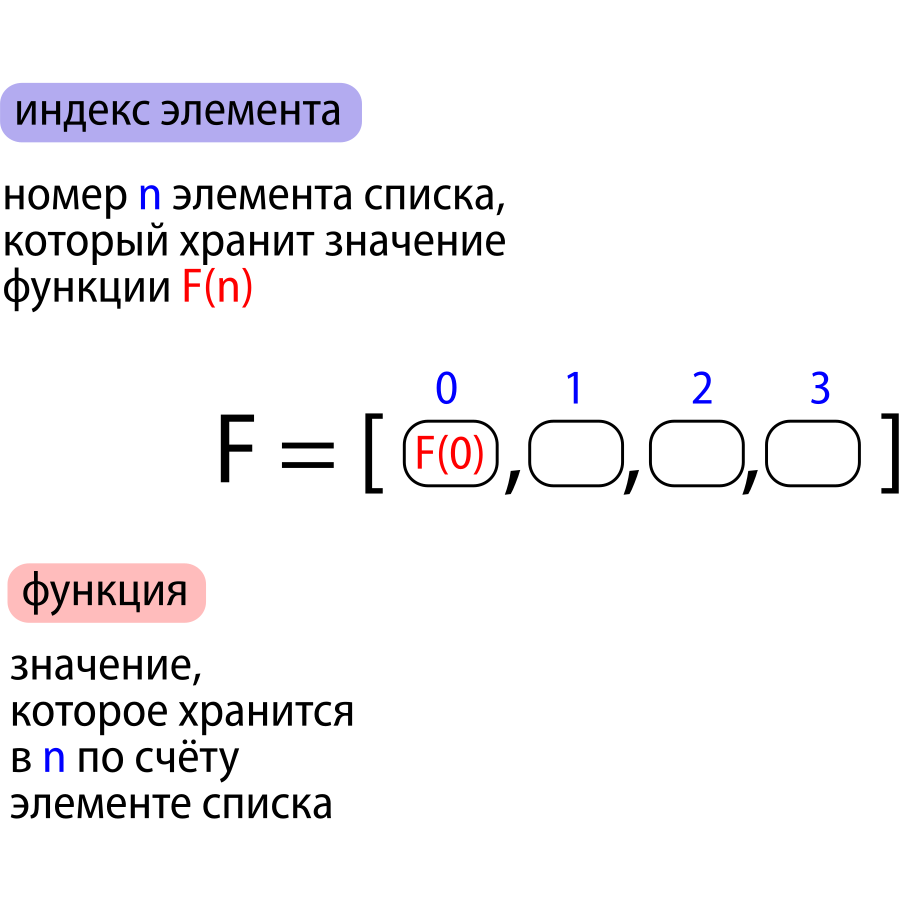
"С номерами 3 и больше" — значит, используем range(3, ...), где на месте многоточия ставим номер последнего интересующего нас элемента + 1
Значения из range(3, ...) мы будем записывать в n, то есть n будет меняться от 3 и до того, что нам нужно
Чтобы n постоянно перезаписывалась, помещаем всё это в цикл for
На данный момент имеем:
for n in range(3, ...):"вписываем значения" — значит, используем метод добавления в конец списка — F.append()
Вписываем мы в конец то, что вычисляется по формуле F(n-1) * n ; помним, что F(n-1) хранится в нашем списке F на месте n-1 то есть тут — F[n-1]
Получается так: F.append( F[n-1] * n )
В итоге имеем такую полную программу:
F = [0, 1, 3]
for n in range(3, ...):
F.append(F[n-1] * n)И теперь, если в задании нам необходимо найти значение функции F(120), мы просто в конце пишем print(F[120])
При этом не забываем, что тогда 2 аргумент в range() должен быть на 1 больше — range(3, 121)
Общая структура кода:
❶ file = open("...").readlines()
❷ A = [int(x) for x in file]
❸ for x in range(...):
...
❹ if ... :
❺ B.append()
❻ print(...) ❶ — открываем файл при помощи команды open() и считываем содержимое при помощи команды readlines(). Команда readlines() создаёт список, заполненный объектами из файла, причём это объекты не типа int(), даже если файл состоял из чисел.
❷ — чтобы получить удобный для работы список, преобразуем каждый его элемент в тип int(). Сохраняем полученный список в переменную A, например.
❸ — очень важный шаг — перебор всевозможных пар последовательности A
Есть 2 типа 17 заданий:
-
где пара — 2 идущих подряд элемента
-
где пара — 2 любых элемента
1 — в этом случае, если один элемент под номером x — A[x], то соседний элемент с номером на 1 больше — A[x+1]. x — это номер элемента, он меняется в диапазоне range(len(A)-1). "-1" появляется, чтобы мы не вышли за пределы списка A.
for x in range(len(A) - 1):
... A[x] ... A[x+1] ... Так и не понял, почему для x именно такой range()?
Посмотрим на список A = [a, b, c, d]
Каждый элемент списка A имеет свой номер, индекс.
Пары состоят из элементов с такими номерами:
- 0 и 1
- 1 и 2
- 2 и 3
Какая взаимосвязь между номерами? — Они отличаются друг от друга на 1.
Значит, мы можем выразить один номер через другой. Пусть номер 0 = х, тогда номер 1 = x + 1 — на один больше.
В каком диапазоне тогда меняется х? Видим что от 0 до 2.
Как перебрать числа из диапазона от 0 до 2? — Пишем range(0, 3) или range(3).
Если список будет больше, то и 2 аргумент в range() будет больше, разумеется — между длиной списка и количеством номеров есть связь. Длина нашего списка, len(A) равна 4, а внутри range(3) аргумент равен 3.
Значит range(3) = range(len(A)-1).
Мы знаем, как меняются номера элементов в паре — теперь можно записать сами элементы.
Это элемент списка A под номером x — A[x] и элемент А под номером х+1 — A[x+1], где х меняется от в диапазоне range(len(A)-1).
х меняется и подставляется в A[x] и A[x+1] — значит используем цикл for, конечно же:
A = [a, b, c, d]
for x in range(0, len(A)-1):
... A[x] ... A[x+1] ...2 — в этом случае нам необходимо 2 независимых переменных, например, x, y: одна (x) отвечает за номера для 1 элемента пары, вторая (y) — за номера для 2 элемента пары.
Ещё неплохо бы перебирать пары без повторов, не брать одну и ту же пару 2 раза.
Если это учесть, структура для перебора пар из 2 любых элементов A будет такая:
for x in range(len(A)):
for y in range(x+1, len(A)):
... A[x] ... A[y] ...❹ — дальше проверяем элементы пары по условию, тут всё довольно легко.
Если проверяем делимость разности, стоит взять модуль этой разности при помощи abs().
❺ — если пара подошла, добавляем нечто в новый, созданный для этого список, например, B.
То, что добавляем, зависит от того, что хотим найти.
Например, мы хотим найти максимальную из сумм элементов пар. Это делалось бы в одну команду max(), если бы у нас был список с суммами элементов пар. Значит, чтобы этот список был, на этом этапе добавляем сумму элементов пар:
B.append(A[x] + A[x+1])или, если пара — 2 любых элемента
B.append(A[x] + A[y])абсолютно аналогично добавляем разность элементов (берём её модуль), сумму квадратов элементов и остальное
❻ — в самом конце делаем вывод.
Например, нужно вывести количество подходящих пар.
Поскольку всегда, когда пара подходила, мы добавляли что-то в список B, то количество элементов в списке B равно количеству подходящих пар.
Итак, количество подходящих пар находится так: len(B).
Ещё нужно найти, например, максимальную разность элементов — если мы добавляли в B разности элементов на этапе ❺, то найти её можно в одну команду max(B).
Алгоритм решения классического 18 задания:
❶ — копируем табличку
❷ — удаляем в скопированной нижней табличке всё, кроме клетки, откуда мы начинаем движение по условию
❸ — пишем функцию и заполняем 1 строку и 1 столбец
❹ — пишем функцию и заполняем всё остальное пространство с учётом стен
❺ — рядом со стенами появляются места, которые в которые мы не можем попасть, как в остальные клетки таблицы — эти ячейки ведут себя как ячейки 1 строки или 1 столбца. Поэтому заполняем их такими же функциями
Рассмотрим типичное условие:
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
❶ — Копируем нашу табличку, для этого можно её выделить (для этого можно нажать Ctrl + A), и с зажатым Ctrl перетянуть, держа её за границу. Как-то так:
Обрати внимание, как меняется вид курсора при зажатии Ctrl.
После этого обводим таблицу в рамку, просто чтобы видеть её границы.
❷ — по условию робот движется из левой верхней в правую нижнюю, значит оставляем её, а всё остальное в скопированной нижней таблице удаляем
❸ — заполняем 1 столбец.
В каждую ячейку 1 столбца мы можем попасть только из верхней (потому что доступные команды только → и ↓).
Поэтому в ячейки 1 столбца мы пишем функцию вида:
- берём собственное значение этой ячейки (из верхней таблицы)
- прибавляем к нему значение ячейки выше
Например, в A14 мы напишем =A2 + A13.
Заметь, что в нашей функции 1 ячейка из 1 таблицы, другая — из 2.
Абсолютно аналогично выглядит функция для ячеек из 1 строки:
- берём собственное значение этой ячейки из верхней таблицы
- прибавляем к нему значение ячейки слева
Например, в B13 мы пишем = B1 + A13.
❹ — Заполняем оставшиеся после заполнения 1 строки и 1 столбца ячейки.
Функцию пишем так:
=- потом берём значение этой ячейки из верхней таблицы и...
- ...прибавляем к нему максимальное из соседних ячеек при помощи
МАКС().
Соседние ячейки — это те, из которых мы можем попасть в данную; они определяются существующими командами.
Здесь всего 2 команды: вправо и вниз, поэтому соседних для данной ячеек всего 2 и они находятся выше неё и левее неё.
Будь аккуратен, иногда команд 3, а значит и в данную ячейку мы можем попасть из 3 ячеек — значит в МАКС() тоже будет 3 аргумента.
Например, команда в B14 такая: =B2 + МАКС(A14; B13).
Обрати внимание, что в функции 1 ячейка из 1 таблицы, а остальные 2 — из 2.
Потом убираем рядом со стенами те ячейки, куда мы можем попасть только из верхней (↓) или только из левой (→). В этих ячейках будет абсолютно та же по структуре формула, что и в 1 столбце, и в 1 строке.
❺ — теперь заполняем эти особые ячейки возле стен.
Они заполняются абсолютно так же, как ячейки 1 столбца и 1 строки.
Поэтому, заполняя пустую строку, мы можем просто скопировать формулу любой средней ячейки из 1 строки.
Так и делаем — кликаем на любую среднюю ячейку из 1 строки, нажимаем Ctrl + C, после этого вокруг ячейки появляется пунктир, вставляем на нужное место (у нас F16), растягиваем на оставшиеся ячейки строки.
При таком копировании, мы копируем именно формулу, а не просто число, так что всё будет работать отлично.
Абсолютно аналогично делаем с ячейками в пустом столбце.
Готово, теперь в нижнем правом углу имеем часть ответа — максимальную сумму, которую можно собрать.
Найти минимальную сумму теперь несложно — просто везде меняем МАКС() на МИН().
Для этого нажимаем Ctrl + F или на главной вкладке выбираем справа кнопку "Найти и выделить" с лупой.
Вот и всё, получили 2 числа — минимальную и максимальную сумму. Записываем в ответ вначале максимальную сумму, потом минимальную без пробела между ними.
В нашем случае ответ: 1131421.
Типичная табличка для 22 задания:
Решение 22 задания с табличкой очень простое. Нам всегда нужно найти минимальное время, за которое выполняться все процессы из таблицы.
Для начала пару простых вещей:
-
время выполнения нескольких процессов не может быть короче времени самого длинного из них
-
если для процесса в 3 колонке указано число 0 — значит такой процесс вообще ни от чего не зависит, полное время его выполнения совпадает со временем из 2 колонки
-
если для процесса в 3 колонке указано несколько номеров процессов — берём из них тот, который будет выполняться самое большое время. При этом наш процесс из 1 столбца будет от него зависеть — значит его полное время = собственное время из 2 колонки + время самого длинного процесса из 3 колонки
-
полное время выполнения процесса будем писать в 4, созданном нами столбце.
На примере данной таблички заполнение 4, созданного нами стобца, будет происходить так:
1 процесс: в 3 колонке у нас 0 — т.е. процесс 1 ни от чего не зависит.
Значит, пишем в созданный столбец его собственное время из 2 колонки — 4
2 процесс: аналогично 1 процессу, для него пишем 3
3 процесс: он зависит от 1 и 2 процессов, выбираем из них самый длинный, т.е. 1 и пишем в созданный нами столбец 4 + 1, т.е. 5 — время 1 процесса + собственное время
4 процесс: он зависит от 3 процесса, значит в нашу созданную колонку пишем 5 + 7, т.е. 12
Из полученных 4 значений полного времени процесса выбираем наибольшее — т.к. раньше система не сможет завершиться — это и есть ответ.
В нашем случае это 12.
Типичный код для решения 23 задания, написан для доступных ходов:
- "+1"
- "+2"
❶ def f(a, b):
❷ if a > b:
return 0
❸ if a == b:
return 1
❹ if a < b:
return f(a+1, b) + f(a+2, b)
❺ print(f(2, 43)) ❶ — создаём функцию f, которая будет зависеть от 2 аргументов: a, b. Первый аргумент a обозначает стартовую позицию, второй аргумент b — конечную позицию. Эта функция считает, сколько существует путей из a в b.
❷ — эта строка определяется доступными ходами. В нашем случае (+1, +2) за ход число может только увеличиться. Значит, невозможно из большего числа попасть в меньшее — поэтому return 0
❸ — эта строка практически во всех заданиях одинаковая. Получается, если мы попали из стартового значения в конечно, функции присваивается 1.
❹ — а вот здесь всегда самая длинная запись. Если стартовая позиция меньше конечной, значит, мы можем использовать наши ходы. При этом мы будем увеличивать наше стартовое число a → a+1 или a → a+2. Конечно же, при этом конечное число b не меняется.
❺ — в конце выводим количество нужных путей, например, количество путей из 2 в 43.
Код для решения разных 24 заданий может довольно сильно отличаться.
Единственное — открытие файла при помощи open() и считывание при помощи .readline() есть всегда.
file = open("24.txt").readline()При этом помни: если файл состоит всего из 1 строки — используешь .readline(), из многих строк — используешь .readlines().
Интересное задание и его решение.
Файл состоит из строк разной длины. Строки содержат только латинские буквы ABC...YZ. Необходимо:
- найти строку, где меньше всего "G"
- определить, какая буква в этой строке встречается чаще
Решение:
❶ — открываем и прочитываем наш файл:
F = open("24.txt").readlines()Важно:
- сохраняешь файл
.pyс программой в том же месте, где и файл"24.txt" - используешь
.readlines(), потому что файл состоит не из 1 строки
❷ — метод .readlines() создаёт список из отдельных строк в файле.
Можем на основании него создать список, состоящий из количеств букв "G" в каждой строке.
То есть:
- берём строку из
F - вычисляем количество
"G"в ней - закидываем полученное число в новый список, например, в
B.
for x in F:
B.append(x.count("G"))или используя генератор:
B = [x.count("G") for x in F]На данном этапе имеем 2 списка такого вида:
F = [AGGGA, G, BGG]
B = [3, 1, 2]❸ — список B получен на основании списка F, значит, номер наименьшего элемента в B равен номеру строки с наименьшим количеством "G" в F.
Что мы делаем:
- берём наименьший элемент из
B—min(B) - находим номер этого элемента —
B.index(min(B)) - этот номер совпадает с номером нужной строки из
F, возьмём еёF[B.index(min(B))]и сохраним в новую переменную, скажем,S
S = F[B.index(min(B))]❹ — теперь осталось найти самую распространённую букву из S:
- берём по очереди все буквы из
S, а лучше не все, а каждую букву только в 1 экземпляре — для этого используемset(S)
for x in set(S):- находим, сколько раз эта буква встречается в
S, выводим это число. Таким образом, мы сразу увидим, какая буква встречается чаще
for x in set(S):
print(S.count(x), x)Даже с set() будет выведено довольно много букв, можно уменьшить количество выводимых данных — например, выводить только те, количество которых > 1500:
for x in set(S):
if S.count(x) > 43:
print(S.count(x), x)Итак, вот полный код:
❶ F = open("24.txt").readlines()
❷ B = [x.count("G") for x in F]
❸ S = F[B.index(min(B))]
❹ for x in set(S):
if S.count(x) > 43:
print(S.count(x), x)Алгоритм поиска делителей числа x:
x = 100
❶ D = []
❷ for y in range(1, int(x**0.5) + 1):
❸ if x % y == 0:
D.append(y)
❹ D.append(x // y)❶ — создаём список D, он будет хранить в себе все делители числа x
❷ — по очереди берём все потенциальные делители числа x, то есть числа от 1 до y, то сразу можем найти парный с ним — x // y.
❸ — проверяем, является ли данный y делителем числа x.
Если да — закидываем y в список D.
❹ — важно: не забываем закинуть в D парный с y элемент, то есть x // y. Не обязательно делить нацело //.
Самое основное для решения заданий на маски
-
на место ✻ можно подставлять любое количество цифр, в том числе можно ничего не подставлять
-
на место ? можно подставить ровно 1 любую цифру
Типичное задание:
Среди натуральных чисел, не превышающих
$10^8$ , найдите все числа, соответствующие маске$12✻4?65$ и делящиеся на 141 без остатка.
Решение:
Число не должно превышать
Разумеется, стандартный шаг — поставить на места всех пропусков переменные, например, x и y, для каждой переменной создать цикл, и собрать число a.
Поскольку на месте ✻ можно поставить не больше 2 цифр, то переменную x мы берём из range(100), не больше.
Например, код ниже подставляет на место ✻ все однозначные и двузначные числа.
for x in range(100):
for y in range(10):
a = int("12" + str(x) + "4" + str(y) + "65")Ещё нужно не забыть, что на место ✻ мы можем вообще не подставлять ничего.
Значит, остаётся только y:
for y in range(10):
a = int("12" + str(x) + "4" + str(y) + "65")И последнее, на место ✻, то есть x можно подставлять ещё числа вида 01, 02, ...
Для этого можно просто перебирать x из range(10), только спереди прибавлять "0", либо же использовать метод .zfill(2) (аргумент 2 потому, что с вместе 0 полученное число будет двузначным)
for x in range(10):
for y in range(10):
a = int("12" + "0" + str(x) + "4" + str(y) + "65")По заданию нам необходимо посчитать такие числа a, которые делятся на 141, поэтому итоговый код такой:
k = 0
❶ for x in range(100):
for y in range(10):
a = int("12" + str(x) + "4" + str(y) + "65")
if a % 141 == 0:
k += 1
❷ for y in range(10):
a = int("12" + str(x) + "4" + str(y) + "65")
if a % 141 == 0:
k += 1
❸ for x in range(10):
for y in range(10):
a = int("12" + "0" + str(x) + "4" + str(y) + "65")
if a % 141 == 0:
k += 1
print(k) С
-
❶ подставляем вместо ✻ все однозначные и двузначные числа
-
❷ ничего не подставляем
-
❸ подставляем числа с незначащим нулём:
01,02,03, ...
В 3 блоке вместо "0" + str(x) можно записать str(x).zfill(2)
- команда ввода
input()- по умолчанию вводит всё как текст, если хотим число — нужно преобразовать
- вывод —
print()
- числа
- целые —
int() - не целые —
float()
- целые —
- текст, строки —
str() - списки —
list() - логический тип —
bool()
Тип определяет операции, которые можно делать с объектом. Строки нельзя делить, например.
Очень полезный тип данных — set(), множества.
Этот тип используем, когда нужно быстро найти что-то среди большого количества данных.
Фишки set():
-
позволяет убрать все повторы в наборе:
set([1, 2, 1, 1]) ⟶ {1, 2}
-
позволяет искать элемент в наборе гораздо быстрее:
x in A — долго x in set(A) — быстро
целые числа int() и нецелые float():
//— берём целую часть от деления%— берём остаток от деления (с отрицательными числами работает не совсем так, лучше бери их модуль)**— возведение в степень
- в конце строки с
ifвсегда: - действия, которые выполняются, только если ... — всегда с отступом после строки с
if
if <условие> :
<действие>"если" — это if, "а если не так" — это else:
if число % 2 == 0:
print("чётное")
else:
print("нечётное")- В том случае, когда "а если не так" — подразумевает несколько вариантов, выбираем конкретный при помощи
elif. Например, условие "число делится на 3". И если мы захотим проверить, делится ли число на 2, мы пишем неelse, аelif, потому что делимость на 2 — не противоположное условие к делимости на 3.
Итог: если 2 противоположных результата — if и else, если есть результат и много других — if и elif.
for <x> in <набор> :
<действия>-
в конце строки с
forвсегда: -
цикл
forпозволяет повторить<действия>сколько-то раз; количество повторов определяется длиной<набора> -
в качестве
<набора>может быть любой объект, у которого можно извлечь отдельные элементы
Примеры наборов, которые состоят из одинакового количества элементов, поэтому дадут одинаковое количество повторов в цикле for:
1, 2, 3
"1", 5//2, 6.0
"a", "b", "c"
"abc"
range(3)
range(0, 3)Полезная штука — генератор списка:
[ <выражение> for <x> in <набор> ]<выражение> определяет, что будет помещено в список [];
<выражение> выполняется для всех <x> в <наборе>
Пару примеров:
[int(x) for x in str(123)][1, 2, 3]
[ 0 for x in range(2) ][0, 0]
[ x**0.5 for x in [4, 9, 16] ][2.0, 3.0, 4.0]
Основные операции со строками:
-
+— склеивание строк:"a" + "a"⟶"aa" -
*— позволяет записать"a" + "a"проще — вот так:"a" * 2 -
срезы, берём элементы строки по их номерам:
"abcd"[0] ⟶ "a"
"abcd"[1:2] ⟶ "b"
"abcd"[1:3] ⟶ "bc"
"abcd"[-1] ⟶ "d"
"abcd"[::-1] ⟶ "dcba"inпозволяет понять, находится ли что-то в строке:
"a" in "abc" ⟶ TrueОсновные методы строк:
-
.find()аргумент — символ, номер которого в строке ищем (будет выведен номер первого найденного элемента слева, иногда полезно искать элемент справа — в этом случае используем.rfind()) -
.count()аргумент — символ, количество которых ищем -
.split()аргумент — символ, по которому делится исходная строка и записывается в список; если аргумент не пишем, по умолчанию делится по пробелампример
A = "a b c".split() print(A)
["a", "b", "c"] -
.replace()1 аргумент — что берём, 2 аргумент — на что заменяем (ещё есть 3 аргумент — сколько найденных элементов заменяем) -
.zfill()позволяет дописать незначащие нули спереди; его аргумент — итоговое количество символов. Можно использовать в 25 задании."2".zfill(3) ⟶ "002" "9".zfill(1) ⟶ "9"
Важно: методы к строкам мы применяем именно так:
строка = строка.метод()Всё потому, что строка — неизменяемый тип.
Применяя к ней метод, мы работаем уже не со строкой (её невозможно изменить), а с её копией; исходная строка в процессе никак не меняется.
Чтобы её изменить, мы перезаписываем в переменную строка вместо строки её изменённую копию.
По этой же причине невозможно изменить элемент строки:
s = "abc"
s[0] = "b"ошибка
Списки можно складывать и умножать на целое число, как строки:
[1] + [2] ⟶ [1, 2]["a"] * 3 ⟶ ["a", "a", "a"]Можно брать отдельные элементы списка и срезы
Методы списков:
-
.append()добавляет элемент в конец списка -
.count()считаем, сколько есть таких элементов в списке -
.sort()расставляет элементы списка по возрастанию; причём работает не только со списками из чисел, но и с текстовыми списками, поскольку все буквы тоже имеют свой номер
Список — это изменяемый тип данных. Когда мы применяем метод к списку, то меняется сам список. Поэтому применение метода к списку выглядит так (сравни со строками):
список.метод()Итог: никогда, применяя к списку метод, не пиши в этой же строке =.
И никогда не применяй методы к списку внутри print()
Самое основное:
-
открытие файла —
open("..."). Пишем полное название файла с расширением, при этом важно, чтобы код находился в той же папке, что и файл, иначе придётся писать весь путь к файлу. -
считывание содержимого файла:
-
.readlines()— если в файле много строк -
.readline()— если в файле только одна строка, или мы хотим считать только 1 строку
-
Как мы работаем с файлом во встроенном приложении IDLE Python:
Алгоритм крайне прост:
❶ — сохраняем файл при помощи Сохранить как (в реальной среде, где пишем ЕГЭ, будет нечто похожее).
Важно: сохраняем файл туда, где собираемся сохранить программу .py с кодом.
Самое простое — сохранять абсолютно всё на рабочий стол
❷ — запускаем IDLE Python (100 % будет у каждого), для этого нажимаем эмблему Windows и просто начинаем писать название — IDLE Python. Откроется главное окно, тут будут выводиться результаты работы программы.
❸ — после открытия IDLE Python создаём новый файл, где и будем писать код.
Для этого нажимаем File ⟶ New File.
Тут мы можем писать наш код, после написания обязательно его сохраняем.
❹ — после сохранения кода (для этого можно использовать Ctrl + S) запускаем код — для этого выбираем Run ⟶ Run Module (или нажимаем F5).
После запуска нас перекинет на главное окно программы, и мы увидем результат работы программы.
invalid syntax
| Что означает? | Ошибка синтаксиса — где-то пропущен или стоит не в том месте : или , или () или ещё другой похожий символ |
|---|---|
| Как исправить? | Нужно поставить : в конце строки с if или for, добавить парную скобку (), поставить , где мы перечисляем разные элементы, например, в print() |
| Где может быть? | Везде |
unexpected indent
| Что означает? | Неожиданный отступ — отступ без какой-либо причины |
|---|---|
| Как исправить? | Просто убрать этот отступ |
| Где может быть? | Везде |
index out of range
| Что означает? | Выход за пределы набора — мы пытаемся взять из набора элемент под слишком большим номером |
|---|---|
| Как исправить? | Поменять 2 аргумент в range() на такое число, каким может быть номер последнего элемента в наборе (в строке, списке и т.д.) |
| Где может быть? | Везде, где работаем с наборами (строками, списками и т.д.) при помощи функции range() и цикла for |
unsupported operand type(s)...
| Что означает? | Неподдерживаемая операция — мы пытаемся делать с объектом что-то невозможное, например, складываем строку с числом |
|---|---|
| Как исправить? | Если операция должна быть именно такая, нужно преобразовать всё, к чему она применяется, в один тип |
| Где может быть? | Везде |
No such file or directory
| Что означает? | Не найден файл, который мы пытаемся открыть |
|---|---|
| Как исправить? | Важно правильно написать внутри функции open() имя файла. Если файл находится в той же папке, что и программа, то имя — это просто полное название файла вместе с расширением (например, вместе с функцией выглядит так: open("17.txt")) |
| Где может быть? | Везде, где есть работа с файлами и используется функция open, например, в 17 и 24 |
max() arg is an empty sequence
| Что означает? | Пытаешься выбрать максимальный элемент из пустого набора, списка |
|---|---|
| Как исправить? | Вся проблема в условии, где-то не заполняется список; нужно переделать условие или создать список в правильном месте |
| Где может быть? | Везде, где список заполняется по каким-то правилам |
5 задание
Текст задания
На вход алгоритма подаётся натуральное число N. По нему строится число R так:
-
Строится двоичная запись числа N.
-
Складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа)
-
шаг 2 повторяется ещё раз для полученной записи
Полученная таким образом запись — двоичная запись искомого числа R. Укажи наименьшее число N, для которого результат работы данного алгоритма больше числа 77.
❶ for N in range(1, 100):
❷ N2 = bin(N)[2:]
❸ a = str(N2.count("1") % 2)
❹ N2 = N2 + a
❺ R = int(N2, 2)
❻ if R > 77:
❼ print(N)
❽ break❶ — почему берём N именно из такого диапазона?
Можно ли было написать range(-100, 100)?
Что делать, если программа написана идеально, но ничего не выводит? Как нужно изменить range()?
❷ — что делает функция bin()?
Какого типа она выдаёт результат?
Для чего с результатом делать [2:]?
❸ — что делает метод .count() в данном случае?
Для чего мы потом % 2?
Зачем тут используем str()?
❹ — что тут происходит?
❺ — что делает функция int(..., 2)?
Что бы мы писали, если бы N2 было 7-ричным числом?
❻ — что мы тут проверяем и зачем?
❼ — почему выводим N, а не R или не N2?
❽ — для чего писать break?
А когда его писать не нужно?
8 задание
12 задание
14 задание
15 задание
16 задание
17 задание
24 задание
Создание и вывод числа
#include <iostream>
using namespace std;
int main(){
int x;
x = 5;
cout << x;
}Ввод числа и его вывод
#include <iostream>
//#include <string>
using namespace std;
int main(){
int n;
cin >> n;
cout << n;
return 0;
}Ввод 2 чисел и их обработка
#include <iostream>
using namespace std;
int main(){
int x;
int y;
cin >> x;
cin >> y;
cout << x+y << endl;
}Спрашивает имя и выводит
#include <iostream>
#include <string>
int main(){
std::string name;
std::cout << "What is your name? ";
getline (std::cin, name);
std::cout << "Hello, " << name << "!";
}№ 6760 Апробация 10.03.23
#include <iostream>
//#include <vector>
#include <cmath>
using namespace std;
int main(){
int n = 6;
int N[] = {1, 2, 5, 7, 8, 10};
int P[] = {100, 200, 4, 3, 2, 190};
int K[6];
for(int i=0; i<6; i++){
K[i] = P[i]/96 + (P[i]%96 > 0);
}
int all_s[6];
for(int x=0; x<6; x++){
int s = 0;
for(int y=0; y<6; y++){
s += abs(N[x] - N[y]) * K[y];
}
all_s[x] = s;
}
int min_s = all_s[0];
for(int i=1; i<6; i++){
if(all_s[i] < min_s){
min_s = all_s[i];
}
}
cout << min_s;
}№ 6760 Апробация 10.03.23 - работа с файлом
#include <iostream>
#include <fstream>
#include <vector>
#include <cmath>
using namespace std;
int main() {
ifstream input("27_A_6760.txt");
int n;
input >> n;
vector<int> N(n);
vector<int> K(n);
for(int i=0; i<n; i++){
int num, prob;
input >> num >> prob;
N[i] = num;
K[i] = prob/48 + (prob%48 > 0);
}
vector<int> all_s(n);
for(int x=0; x<n; x++){
int s = 0;
for(int y=0; y<n; y++){
s += abs(N[x] - N[y]) * K[y];
}
all_s[x] = s;
}
int min_s = all_s[0];
for(int i=1; i<n; i++){
if(all_s[i] < min_s){
min_s = all_s[i];
}
}
cout << min_s;
return 0;
}